题目内容
当太阳光线与地面成45o角时,在坡度为i="1:2" 的斜坡上的一棵树AB落在坡面上的影子AC长为5米,落在水平线上的影子CD长为3米,求这棵树的高度(参考数据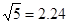 ,
,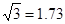 ,
, ,结果保留两个有效数字).
,结果保留两个有效数字).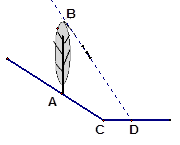
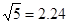 ,
,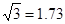 ,
, ,结果保留两个有效数字).
,结果保留两个有效数字).
5.2
首先把实际问题转化为直角三角形问题,延长DC和BA交于点E,先由直角三角形ACE及已知坡度为i=1:2的斜坡求出AE和CE,再由直角△BED求出BE,从而求出这棵树AB的高度.
: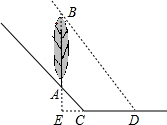
解:延长DC和BA交于点E,
设AE=x,则由坡度为i=1:2的斜坡得,CE=2x,
∴x2+(2x)2=52,
由实际问题解得:
x= √5
∴AE= √5 ,CE=2 √5
则ED=3+2 √5
∴BE=ED?tan60°=(3+2 √5)* √3="3" √3+2 √15
∴AB=BE-AE=3 √3+2 √15-√5=5.2
:

解:延长DC和BA交于点E,
设AE=x,则由坡度为i=1:2的斜坡得,CE=2x,
∴x2+(2x)2=52,
由实际问题解得:
x= √5
| |
则ED=3+2 √5
| |
∴AB=BE-AE=3 √3+2 √15-√5=5.2

练习册系列答案
相关题目
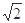 ≈1.41、
≈1.41、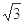 ≈1.73、 sin75°≈0.97、cos75°≈0.26、tan75°≈3.73)
≈1.73、 sin75°≈0.97、cos75°≈0.26、tan75°≈3.73)
 如图放置,点A,B,C都在格点上,则sin∠BAC的值为 ( )
如图放置,点A,B,C都在格点上,则sin∠BAC的值为 ( )




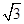 ≈1.732)
≈1.732)



 的值是( )
的值是( )




