题目内容
【题目】晚饭后,小聪和小军在社区广场散步,小聪问小军:“你有多高?”小军一时语塞.小聪思考片刻,提议用广场照明灯下的影长及地砖长来测量小军的身高.于是,两人在灯下沿直线NQ移动,如图,当小聪正好站在广场的A点(距N点5块地砖长)时,其影长AD恰好为1块地砖长;当小军正好站在广场的B点(距N点9块地砖长)时,其影长BF恰好为2块地砖长.已知广场地面由边长为0.8米的正方形地砖铺成,小聪的身高AC为1.6米,MN⊥NQ,AC⊥NQ,BE⊥NQ.请你根据以上信息,求出小军身高BE的长(结果精确到0.01米).
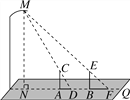
【答案】小军身高BE的长约为1.75米.
【解析】试题分析:先利用相似三角形的性质求出MN的长度,再利用相似三角形的性质求出EB的长度就可.
试题解析:有题意可知∠CAD=∠MND="90°," ∠CDA=∠MDN
∴△CAD≌△MND ∴![]() 即
即![]() ∴ MN=9.6
∴ MN=9.6
又∵∠EBF=∠MNF="90°," ∠EFB=∠MNF
∴△EBF≌△MNF ∴![]() 即
即![]() ∴ EB=1.75
∴ EB=1.75
所以小军身高BE的长为1.75米.

练习册系列答案
相关题目