Question

在平面直角坐标系中给定以下五个点A（-3，0），B（-1，4），C（0，3），D（

1

2

，

7

4

），E（1，0）．
（1）请从五点中任选三点，求一条以平行于y轴的直线为对称轴的抛物线的解析式；
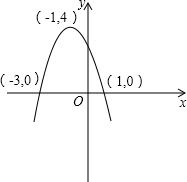
（2）求该抛物线的顶点坐标和对称轴，并画出草图．

Answer 1

分析：（1）设抛物线的解析式为y=ax²+bx+c，设这个二次函数过A（-3，0），C（0，3），E（1，0）三点，分别代入解析式，列方程组求解即可；
（2）将二次函数解析式配方为顶点式，可确定顶点坐标及对称轴．

解答：解：（1）设抛物线的解析式为y=ax²+bx+c，且过点A（-3，0），C（0，3），E（1，0），
由（0，3）在y=ax²+bx+c上．则c=3，再将A、E两点坐标代入，
得

9a-3b+3=0 a+b+3=0

，解得a=-1，b=-2．
∴抛物线的解析式为y=-x²-2x+3；

（2）由y=-x²-2x+3=-（x+1）²+4，得
顶点坐标为（-1，4），对称轴为x=-1．

点评：本题考查了待定系数法求二次函数解析式的一般方法，同时考查了二次函数解析式的变形．