题目内容
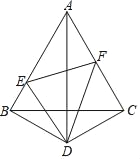
【题目】已知点
、
在
的
边上，
，
，为了判断
与
的大小关系，请你填空完成下面的推理过程，并在空白括号内，注明推理的根据．
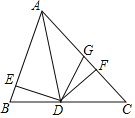
解：作
，垂足为
∵，
∴
是________三角形，
∴
________
又∵，
∴
________，即
________；
又∵________（自己所作），
∴
是线段________的垂直平分线；
∴
________
∴________．
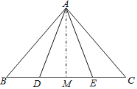
【答案】等腰 底边上的高也是底边上的中线 
线段垂直平分线上的点到线段两个端点的距离相等 
【解析】
首先根据等腰三角形的性质，得DM=EM，结合已知条件，根据等式的性质，得BM=CM，从而根据线段垂直平分线的性质，得AB=AC，再根据等腰三角形的性质即可证明．
作AM⊥BC，垂足为M，
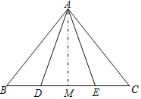
∵AD=AE，
∴△ADE是等腰三角形，
∴DM=EM （等腰三角形底边上的高也是底边上的中线）
又∵BD=CE，
∴BD+DM=CE+EM，即BM=CM，
又∵AM⊥BC（自己所作），
∴AM是线段BC的垂直平分线，
∴AB=AC （线段垂直平分线上的点到线段两个端点的距离相等）
∴∠B=∠C．
故答案为：等腰，等腰三角形底边上的高也是底边上的中线，CE+EM，CM，AM⊥BC，BC，线段垂直平分线上的点到线段两个端点的距离相等，∠B=∠C．
练习册系列答案
相关题目
