题目内容
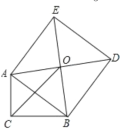
【题目】我们定义:如图1,在△ABC中,把AB绕点A按顺时针方向旋转α(0°<α<180°)得到AB′,把AC绕点A按逆时针方向旋转β得到AC′,连接B′C′,当α+β=180°时,我们称△AB′C′是△ABC的“旋补三角形”,△AB′C′边B′C′上的中线AD叫做△ABC的“旋补中线”,点A叫做“旋补中心”.
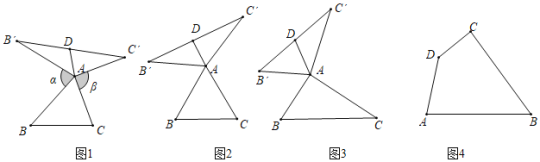
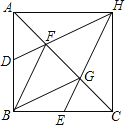
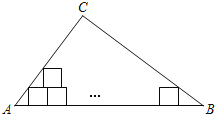
(1)特例感知:在图2、图3中,△AB′C′是△ABC的“旋补三角形”,AD是△ABC的“旋补中线”.
①如图2,当△ABC为等边三角形时,AD与BC的数量关系为AD=______BC;
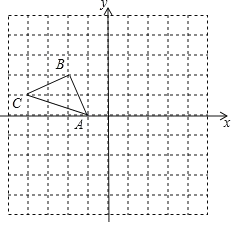
②如图3,当∠BAC=90°,BC=8时,则AD长为______.
(2)精确作图:如图4,已知在四边形ABCD内部存在点P,使得△PDC是△PAB的“旋补三角形”(点D的对应点为点A,点C的对应点为点B),请用直尺和圆规作出点P(要求:保留作图痕迹,不写作法和证明)
(3)猜想论证:在图1中,当△ABC为任意三角形时,猜想AD与BC的数量关系,并给予证明.
【答案】(1)①![]() ,②4;(2)见解析;(3)AD=
,②4;(2)见解析;(3)AD=![]() BC.
BC.
【解析】
(1)①根据含30°直角三角形的性质解答;②证明△AB′C′≌△ABC,根据全等三角形的性质得到B′C′=BC,根据直角三角形的性质计算;
(2)根据线段垂直平分线的性质、利用尺规作图作出点P;
(3)证明四边形AB′EC′是平行四边形,得到B′E=AC′,∠B′AC′+∠AB′E=180°,根据全等三角形的性质得到AE=BC,得到答案.
解:(1)①∵△ABC是等边三角形,
∴AB=AC=BC,∠BAC=60°,
∵△AB′C′是△ABC的“旋补三角形”,
∴∠B′AC′=120°,AB=AB′,AC=AC′,
∴AB′=AC′,
∴∠AB′D=30°,
∴AD=![]() AB′,
AB′,
∴AD=![]() BC,
BC,
故答案为:![]() ;
;
②∵△AB′C′是△ABC的“旋补三角形”,
∴∠B′AC′=∠BAC=90°,AB=AB′,AC=AC′,
在△AB′C′和△ABC中,
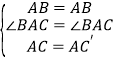 ,
,
∴△AB′C′≌△ABC(SAS)
∴B′C′=BC=8,
∵∠B′AC′=90°,AD是△ABC的“旋补中线”,
∴AD=![]() B′C′=4,
B′C′=4,
故答案为:4;
(2)如图4,作线段AD、BC的垂直平分线,交点即为点P,

∴点P即为所作;
(3)AD=![]() BC,
BC,
证明:如图1,延长AD到E,使得DE=AD,连接B′E、C′E,
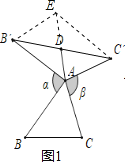
∵AD是△AB′C’的中线,
∴B′D=C′D,
∵DE=AD,
∴四边形AB′EC′是平行四边形,
∴B′E=AC′,∠B′AC′+∠AB′E=180°,
∵α+β=180°,
∴∠B′AC′+∠BAC=180°,
∴∠EB′A=∠BAC,
在△EB′A和△CAB中,
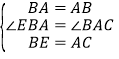
∴△EB′A≌△CAB(SAS),
∴AE=BC,
∴AD=![]() BC.
BC.