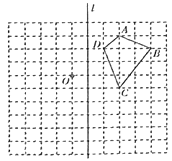
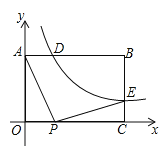
ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§Ηχ≥ω»γœ¬Ε®“ε:“―÷ΣΝΫΗωΚ· ΐΘ§»γΙϊΕ‘”Ύ»Έ“βΒΡΉ‘±δΝΩ![]() ,’βΝΫΗωΚ· ΐΕ‘”ΠΒΡΚ· ΐ÷ΒΦ«ΈΣ
,’βΝΫΗωΚ· ΐΕ‘”ΠΒΡΚ· ΐ÷ΒΦ«ΈΣ![]() , Κψ”–Βψ
, Κψ”–Βψ![]() ΚΆΒψ
ΚΆΒψ![]() ΙΊ”ΎΒψ
ΙΊ”ΎΒψ![]() ≥…÷––ΡΕ‘≥Τ(¥Υ»ΐΗωΒψΩ…“‘÷ΊΚœ)Θ§”…”ΎΕ‘≥Τ÷––Ρ
≥…÷––ΡΕ‘≥Τ(¥Υ»ΐΗωΒψΩ…“‘÷ΊΚœ)Θ§”…”ΎΕ‘≥Τ÷––Ρ![]() ΕΦ‘Ύ÷±œΏ
ΕΦ‘Ύ÷±œΏ![]() …œΘ§Υυ“‘≥Τ’βΝΫΗωΚ· ΐΈΣΙΊ”Ύ÷±œΏ
…œΘ§Υυ“‘≥Τ’βΝΫΗωΚ· ΐΈΣΙΊ”Ύ÷±œΏ![]() ΒΡΓΑœύ“άΚ· ΐΓ±ΓΘάΐ»γ:
ΒΡΓΑœύ“άΚ· ΐΓ±ΓΘάΐ»γ: ![]() ΚΆ
ΚΆ![]() ΈΣΙΊ”Ύ÷±œΏ
ΈΣΙΊ”Ύ÷±œΏ![]() ΒΡ ΓΑœύ“άΚ· ΐΓ±.
ΒΡ ΓΑœύ“άΚ· ΐΓ±.
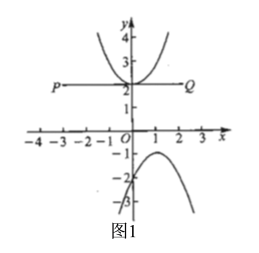
Θ®1Θ©“―÷ΣΒψ![]() «÷±œΏ
«÷±œΏ![]() …œ“ΜΒψΘ§«κ«σ≥ωΒψ
…œ“ΜΒψΘ§«κ«σ≥ωΒψ![]() ΙΊ”ΎΒψ
ΙΊ”ΎΒψ![]() ≥…÷––ΡΕ‘≥ΤΒΡΒψ
≥…÷––ΡΕ‘≥ΤΒΡΒψ![]() ΒΡΉχ±ξ:
ΒΡΉχ±ξ:
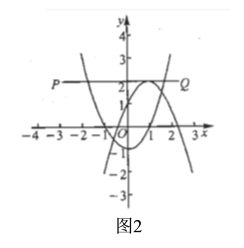
Θ®2Θ©»τ÷±œΏ![]() ΚΆΥϋΙΊ”Ύ÷±œΏ
ΚΆΥϋΙΊ”Ύ÷±œΏ![]() ΒΡΓΑœύ“άΚ· ΐΓ±ΒΡΆΦœσ”κ
ΒΡΓΑœύ“άΚ· ΐΓ±ΒΡΆΦœσ”κ![]() ÷αΈß≥…ΒΡ»ΐΫ«–ΈΒΡΟφΜΐΈΣ
÷αΈß≥…ΒΡ»ΐΫ«–ΈΒΡΟφΜΐΈΣ![]() Θ§«σ
Θ§«σ![]() ΒΡ÷Β;
ΒΡ÷Β;
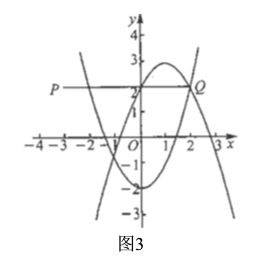
Θ®3Θ©»τΕΰ¥ΈΚ· ΐ![]() ΚΆ
ΚΆ![]() ΈΣΙΊ”Ύ÷±œΏ
ΈΣΙΊ”Ύ÷±œΏ![]() ΒΡΓΑœύ“άΚ· ΐΓ±.
ΒΡΓΑœύ“άΚ· ΐΓ±.
ΔΌ«κ«σ≥ω![]() ΒΡ÷Β;
ΒΡ÷Β;
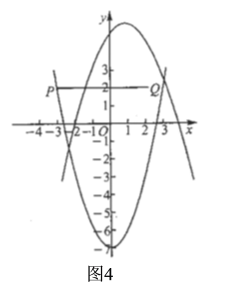
ΔΎ“―÷ΣΒψ![]() ΓΔΒψ
ΓΔΒψ![]() Ν§Ϋ”
Ν§Ϋ”![]() ÷±Ϋ”–¥≥ω
÷±Ϋ”–¥≥ω![]() ΚΆ
ΚΆ![]() ΝΫΧθ≈ΉΈοœΏ”κœΏΕΈ
ΝΫΧθ≈ΉΈοœΏ”κœΏΕΈ![]() ”–ΡΩ÷Μ”–ΝΫΗωΫΜ’Φ ±Ε‘”ΠΒΡ
”–ΡΩ÷Μ”–ΝΫΗωΫΜ’Φ ±Ε‘”ΠΒΡ![]() ΒΡ»Γ÷ΒΖΕΈß.
ΒΡ»Γ÷ΒΖΕΈß.
ΓΨ¥πΑΗΓΩΘ®1Θ©Θ®1Θ§-4Θ©ΘΜΘ®2Θ©![]() ΘΜΘ®3Θ©ΔΌ-1Θ§2 ΘΜ ΔΎ
ΘΜΘ®3Θ©ΔΌ-1Θ§2 ΘΜ ΔΎ![]() Μρ
Μρ![]()
ΓΨΫβΈωΓΩ
Θ®1Θ©œ»«σ≥ωΒψMΒΡΉχ±ξΘ§ΗυΨίΒψM”κΒψNΙΊ”Ύ![]() ≥…÷––ΡΕ‘≥ΤΘ§Φ¥Ω…«σ≥ωΒψNΒΡΉχ±ξΘΜ
≥…÷––ΡΕ‘≥ΤΘ§Φ¥Ω…«σ≥ωΒψNΒΡΉχ±ξΘΜ
Θ®2Θ©…ηΒψ![]() ΚΆΒψ
ΚΆΒψ![]() Ζ÷±π «÷±œΏ
Ζ÷±π «÷±œΏ![]() ”κΥϋΒΡΓΑœύ“άΚ· ΐΓ±ΒΡΆΦœσ…œΒΡ»Έ“β“ΜΒψΘ§ΗυΨίœύ“άΚ· ΐΒΡΕ®“εΘ§Ω…ΒΟΘΚ÷±œΏ
”κΥϋΒΡΓΑœύ“άΚ· ΐΓ±ΒΡΆΦœσ…œΒΡ»Έ“β“ΜΒψΘ§ΗυΨίœύ“άΚ· ΐΒΡΕ®“εΘ§Ω…ΒΟΘΚ÷±œΏ![]() ΙΊ”Ύ÷±œΏy=xΒΡœύ“άΚ· ΐ «ΘΚ
ΙΊ”Ύ÷±œΏy=xΒΡœύ“άΚ· ΐ «ΘΚ![]() Θ§ΫαΚœΓΑ÷±œΏ
Θ§ΫαΚœΓΑ÷±œΏ![]() ΚΆΥϋΙΊ”Ύ÷±œΏ
ΚΆΥϋΙΊ”Ύ÷±œΏ![]() ΒΡΓΑœύ“άΚ· ΐΓ±ΒΡΆΦœσ”κ
ΒΡΓΑœύ“άΚ· ΐΓ±ΒΡΆΦœσ”κ![]() ÷αΈß≥…ΒΡ»ΐΫ«–ΈΒΡΟφΜΐΈΣ
÷αΈß≥…ΒΡ»ΐΫ«–ΈΒΡΟφΜΐΈΣ![]() Γ±Θ§Ν–≥ωΙΊ”ΎnΒΡΖΫ≥ΧΘ§Φ¥Ω…«σΫβΘΜ
Γ±Θ§Ν–≥ωΙΊ”ΎnΒΡΖΫ≥ΧΘ§Φ¥Ω…«σΫβΘΜ
Θ®3Θ©ΔΌ”…œύ“άΚ· ΐΒΡΕ®“εΘ§ΒΟΘΚ![]() Θ§Μ·Φρ’ϊάμΚσΘ§Φ¥Ω…«σΫβΘΜΔΎΖ÷ΥΡ÷÷«ιΩωΜ≠≥ωΕΰ¥ΈΚ· ΐ
Θ§Μ·Φρ’ϊάμΚσΘ§Φ¥Ω…«σΫβΘΜΔΎΖ÷ΥΡ÷÷«ιΩωΜ≠≥ωΕΰ¥ΈΚ· ΐ![]() Θ§
Θ§![]() ΒΡΆΦœσΘ§Φ¥Ω…ΒΟΒΫ¥πΑΗΘ°
ΒΡΆΦœσΘ§Φ¥Ω…ΒΟΒΫ¥πΑΗΘ°
Θ®1Θ©ΓΏΒψ![]() «÷±œΏ
«÷±œΏ![]() …œ“ΜΒψΘ§
…œ“ΜΒψΘ§
Γύ![]() Θ§Φ¥ΘΚ
Θ§Φ¥ΘΚ![]() Θ§
Θ§
ΓΏΒψN”κΒψ![]() ΙΊ”Ύ
ΙΊ”Ύ![]() ≥…÷––ΡΕ‘≥ΤΘ§
≥…÷––ΡΕ‘≥ΤΘ§
Γύ![]() ΘΜ
ΘΜ
Θ®2Θ©…ηΒψ![]() ΚΆΒψ
ΚΆΒψ![]() Ζ÷±π «÷±œΏ
Ζ÷±π «÷±œΏ![]() ”κΥϋΒΡΓΑœύ“άΚ· ΐΓ±ΒΡΆΦœσ…œΒΡ»Έ“β“ΜΒψΘ§
”κΥϋΒΡΓΑœύ“άΚ· ΐΓ±ΒΡΆΦœσ…œΒΡ»Έ“β“ΜΒψΘ§
Γύ![]() Θ§
Θ§
![]() Θ§
Θ§
Γύ÷±œΏ![]() ΙΊ”Ύ÷±œΏy=xΒΡœύ“άΚ· ΐ «ΘΚ
ΙΊ”Ύ÷±œΏy=xΒΡœύ“άΚ· ΐ «ΘΚ![]() Θ§
Θ§
ΝΣΝΔ![]() Θ§ΫβΒΟΘΚ
Θ§ΫβΒΟΘΚ![]() Θ§
Θ§
Γύ÷±œΏ![]() ”κ÷±œΏ
”κ÷±œΏ![]() ΒΡΫΜΒψΒΡΚαΉχ±ξΈΣ
ΒΡΫΜΒψΒΡΚαΉχ±ξΈΣ![]() Θ§
Θ§
ΓΏ÷±œΏ![]() ”κ÷±œΏ
”κ÷±œΏ![]() ”κy÷αΒΡΫΜΒψΉχ±ξΖ÷±π «ΘΚ(0Θ§n)Θ§(0Θ§-n)Θ§
”κy÷αΒΡΫΜΒψΉχ±ξΖ÷±π «ΘΚ(0Θ§n)Θ§(0Θ§-n)Θ§
”…Χβ“βΒΟΘΚ![]() Θ§ΫβΒΟΘΚ
Θ§ΫβΒΟΘΚ![]() ΘΜ
ΘΜ
Θ®3Θ©ΔΌ”…Χβ“βΒΟΘΚ![]() Θ§
Θ§
Γύ![]() Θ§Ε‘”Ύ»Έ“βΒΡxΕΦ≥…ΝΔΘ§
Θ§Ε‘”Ύ»Έ“βΒΡxΕΦ≥…ΝΔΘ§
Γύ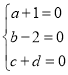 Θ§ΫβΒΟΘΚ
Θ§ΫβΒΟΘΚ![]() ΘΜ
ΘΜ
ΔΎ”…ΒΎΔΌ–ΓΧβΘ§Ω…÷ΣΘΚ![]() Θ§
Θ§![]() Θ§
Θ§
Β±![]() ±Θ§»γΆΦ1Θ§
±Θ§»γΆΦ1Θ§
Β±![]() ±Θ§»γΆΦ2Θ§
±Θ§»γΆΦ2Θ§
Β±![]() ±Θ§»γΆΦ3Θ§
±Θ§»γΆΦ3Θ§
Β±![]() ±Θ§»γΆΦ4Θ§
±Θ§»γΆΦ4Θ§
Ήέ…œΩ…÷Σ:![]() Μρ
Μρ![]() ±Θ§≈ΉΈοœΏ”κœΏΕΈ
±Θ§≈ΉΈοœΏ”κœΏΕΈ![]() ”–«“÷Μ”–ΝΫΗωΫΜΒψΘ°
”–«“÷Μ”–ΝΫΗωΫΜΒψΘ°