题目内容
【题目】有3个完全相同的小球,把它们分别标号为1,2,3,放在一个不透明的口袋中,从口袋中随机摸出一个小球,记下标号后放回,再从口袋中随机摸出一个小球,记下标号.用画树状图(或列表)的方法,求两次摸出的小球号码恰好都大于1的概率.
【答案】解:画树状图得:
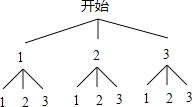
由图可得共有9种等可能的结果,其中两次摸出的小球号码恰好都大于1的有4种结果,
∴两次摸出的小球号码恰好都大于1的概率为 ![]() .
.
【解析】事件分为两个步骤,第一个步骤3种情况,第二个步骤的三种情况和上一层的每种情况对应,共9种机会均等的情况,关注的结果有4种,利用概率公式可求出结果.
【考点精析】关于本题考查的列表法与树状图法,需要了解当一次试验要设计三个或更多的因素时,用列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用树状图法求概率才能得出正确答案.

练习册系列答案
相关题目
【题目】新房装修后,甲居民购买家居用品的清单如下表,因污水导致部分信息无法识别,根据下表解决问题:
家居用品名称 | 单价(元) | 数量(个) | 金额(元) |
挂钟 | 30 | 2 | 60 |
垃圾桶 | 15 | ||
塑料鞋架 | 40 | ||
艺术字画 | a | 2 | 90 |
电热水壶 | 35 | 1 | b |
合计 | 8 | 280 | |
(1)直接写出a= , b=;
(2)甲居民购买了垃圾桶,塑料鞋架各几个?
(3)若甲居民再次购买艺术字画和垃圾桶两种家居用品,共花费150元,则有哪几种不同的购买方案?