题目内容
【题目】若对任意的实数a，函数f（x）=（x﹣1）lnx﹣ax+a+b有两个不同的零点，则实数b的取值范围是（ ）
A.（﹣∞，﹣1]
B.（﹣∞，0）
C.（0，1）
D.（0，+∞）
【答案】B
【解析】解：令f（x）=0得（x﹣1）lnx=a（x﹣1）﹣b， 令g（x）=（x﹣1）lnx，则g′（x）=lnx+1﹣ 
，
∴当0＜x＜1时，g′（x）＜0，当x＞1时，g′（x）＞0，
∴g（x）在（0，1）上单调递减，在（1，+∞）上单调递增，
作出y=（x﹣1）lnx与y=a（x﹣1）﹣b的大致函数图象，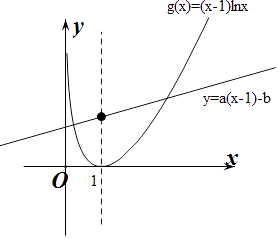
∵f（x）很有两个不同的零点，
∴y=a（x﹣1）﹣b与g（x）=（x﹣1）lnx恒有两个交点，
∵直线y=a（x﹣1）﹣b恒过点（1，﹣b），
∴﹣b＞0，即b＜0．
故选B．
练习册系列答案
全能测控一本好卷系列答案
相关题目
【题目】某网店尝试用单价随天数而变化的销售模式销售一种商品，利用30天的时间销售一种成本为10元/件的商品售后，经过统计得到此商品单价在第x天（x为正整数）销售的相关信息，如表所示：
销售量n（件） | n=50﹣x |
销售单价m（元/件） | 当1≤x≤20时， |
当21≤x≤30时， |
（1）请计算第15天该商品单价为多少元/件？
（2）求网店销售该商品30天里所获利润y（元）关于x（天）的函数关系式；
（3）这30天中第几天获得的利润最大？最大利润是多少？
