Question

【题目】在四棱锥P﹣ABCD中，AD∥BC，AD=AB=DC= BC=1，E是PC的中点，面PAC⊥面ABCD．
（Ⅰ）证明：ED∥面PAB；
（Ⅱ）若PC=2，PA= ，求二面角A﹣PC﹣D的余弦值．

Answer 1

【答案】（Ⅰ）证明：取PB的中点F，连接AF，EF．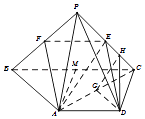
∵EF是△PBC的中位线，∴EF∥BC，且EF= ．
又AD=BC，且AD= ，∴AD∥EF且AD=EF，
则四边形ADEF是平行四边形．
∴DE∥AF，又DE面ABP，AF面ABP，
∴ED∥面PAB；
（Ⅱ）解：法一、取BC的中点M，连接AM，则AD∥MC且AD=MC，
∴四边形ADCM是平行四边形，
∴AM=MC=MB，则A在以BC为直径的圆上．
∴AB⊥AC，可得 ．
过D作DG⊥AC于G，
∵平面PAC⊥平面ABCD，且平面PAC∩平面ABCD=AC，
∴DG⊥平面PAC，则DG⊥PC．
过G作GH⊥PC于H，则PC⊥面GHD，连接DH，则PC⊥DH，
∴∠GHD是二面角A﹣PC﹣D的平面角．
在△ADC中， ，连接AE， ．
在Rt△GDH中， ，
∴ ，
即二面角A﹣PC﹣D的余弦值 ．
法二、取BC的中点M，连接AM，则AD∥MC，且AD=MC．
∴四边形ADCM是平行四边形，
∴AM=MC=MB，则A在以BC为直径的圆上，
∴AB⊥AC．
∵面PAC⊥平面ABCD，且平面PAC∩平面ABCD=AC，∴AB⊥面PAC．
如图以A为原点， 方向分别为x轴正方向，y轴正方向建立空间直角坐标系．
可得 ， ．
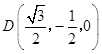设P（x，0，z），（z＞0），依题意有 ， ，
解得 ．
则 ， ， ．
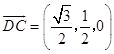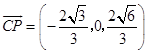设面PDC的一个法向量为 ，
由 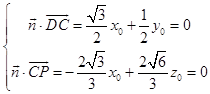，取x0=1，得 ．
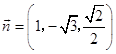为面PAC的一个法向量，且 ，
设二面角A﹣PC﹣D的大小为θ，
则有 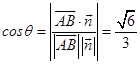，即二面角A﹣PC﹣D的余弦值 ．

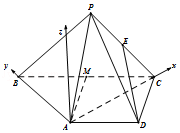
【解析】（Ⅰ）取PB的中点F，连接AF，EF，由三角形的中位线定理可得四边形ADEF是平行四边形．得到DE∥AF，再由线面平行的判定可得ED∥面PAB；（Ⅱ）法一、取BC的中点M，连接AM，由题意证得A在以BC为直径的圆上，可得AB⊥AC，找出二面角A﹣PC﹣D的平面角．求解三角形可得二面角A﹣PC﹣D的余弦值．法二、由题意证得AB⊥AC．又面PAC⊥平面ABCD，可得AB⊥面PAC．以A为原点， 方向分别为x轴正方向，y轴正方向建立空间直角坐标系．求出P的坐标，再求出平面PDC的一个法向量，由图可得 为面PAC的一个法向量，由两法向量所成角的余弦值可得二面角A﹣PC﹣D的余弦值．