题目内容
【题目】已知,直线![]() ,
,![]() 、
、![]() 分别是
分别是![]() 和
和![]() 上的动点,点
上的动点,点![]() 为直线
为直线![]() 、
、![]() 之间任一点,且
之间任一点,且![]() ,则
,则![]() 与
与![]() 之间的数量关系为______.
之间的数量关系为______.
【答案】![]() 或
或![]()
【解析】
分两种情况进行讨论:①过点P作PQ∥AB,根据平行公理可得PQ∥CD,再根据两直线平行,内错角相等可得∠AMP=∠1,∠CNP=∠2,然后根据∠P=∠1+∠2等量代换即可得解;②过点P作PQ∥AB,根据平行公理可得PQ∥CD,再根据两直线平行,同旁内角互补可得∠AMP=180°-∠1,∠CNP=180°-∠2,然后根据∠P=∠1+∠2等量代换即可得解.
解:分两种情况: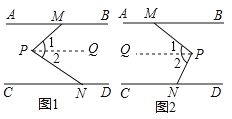
如图1,过点P作PQ∥AB,
∵AB∥CD,
∴PQ∥CD∥AB,
∴∠AMP=∠1,∠CNP=∠2,
∵PM⊥PN,
∴∠MPN=∠1+∠2=90°,
∴∠AMP+∠CNP=90°;
如图2,过点P作PQ∥AB,
∵AB∥CD,
∴PQ∥CD∥AB,
∴∠AMP=180°-∠1,∠CNP=180°-∠2,
∴∠AMP+∠CNP=180°×2-∠1-∠2,
∵∠MPN=∠1+∠2=90°,
∴∠AMP+∠CNP=360°-90°=270°;
综上所述,∠AMP与∠CNP之间的数量关系为:∠AMP+∠CNP=90°或∠AMP+∠CNP=270°.
故答案为:∠AMP+∠CNP=90°或∠AMP+∠CNP=270°.

练习册系列答案
相关题目