题目内容
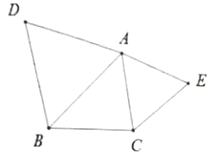
【题目】如图所示，AB∥CD，AD∥BC，BE＝DF，则图中全等三角形共有( )对．
A. 2B. 3C. 4D. 1
【答案】B
【解析】
根据AB∥CD，AD∥BC可得∠ABD＝∠CDB，∠ADB＝∠CBD，结合公共边BD＝DB利用ASA可证ABD≌△CDB；由ABD≌△CDB可得AB＝CD，∠ABD＝∠CDB，结合BE＝DF利用SAS可证△ABE≌△CDF；由ABD≌△CDB，△ABE≌△CDF可得AD＝CB，AE＝CF，求出BF＝DE利用SSS证明△AED≌△CFB，问题得解.
解：①∵AB∥CD，AD∥BC，
∴∠ABD＝∠CDB，∠ADB＝∠CBD，
∵BD＝DB，
∴ABD≌△CDB（ASA）；
②∵ABD≌△CDB，
∴AB＝CD，∠ABD＝∠CDB，
∵BE＝DF，
∴△ABE≌△CDF（SAS）；
③∵ABD≌△CDB，△ABE≌△CDF，
∴AD＝CB，AE＝CF，
∵BE＝DF，
∴BE＋EF＝DF＋EF，即BF＝DE，
∴△AED≌△CFB（SSS）；
所以图中全等三角形共有3对．
故选：B．
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
