题目内容
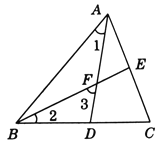
【题目】如图,AB=AC,∠A=36°,AB的垂直平分线MN交AB于点M,交AC于点D,下列结论:①△BCD是等腰三角形;②BD是∠ABC的平分线;③DC+BC=AB;④△AMD≌△BCD,正确的是 ( )

A.①②B.②③C.①②③D.①②④
【答案】C
【解析】
由等腰三角形的性质和垂直平分线的性质,结合三角形的内角和定理,以及全等三角形的判定,分别进行判断,即可得到答案.
解:∵AB=AC,∠A=36°,
∴∠ABC=∠C=![]() ,
,
∵MN垂直平分AB,
∴AD=BD,AM=BM,
∴∠ABD=∠A=36°,
∴∠DBC=36°,∠BDC=72°,
∴BD=BC,
∴△BCD是等腰三角形,①正确;
∵∠ABD=∠DBC=36°,
∴BD平分∠ABC,②正确;
∵BC=BD=AD,AB=AC,
∴DC+BC=DC+AD=AC=AB;③正确;
△AMD与△BCD不能证明全等,④错误;
故正确的结论有:①②③;
故选:C.

练习册系列答案
相关题目