Question

【题目】如图，，点是直线，之间的一点，连接、.

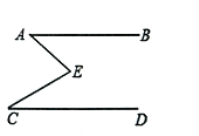
（1）问题发现：

①若，，则 ．

②猜想图中、、的数量关系，并证明你的结论.

（2）拓展应用:

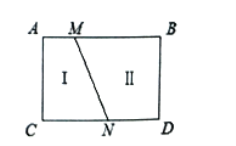
如图，，线段把这个封闭区域分为、两部分（不含边界），点是位于这两个区域内的任意一点（不在边界上），请直接写出、、的数量关系.

Answer 1

【答案】（1）①，②，见解析；（2）当点位于区域时， ，当点位于区域时， .

【解析】

（1）①过点E作EF∥AB，再由平行线的性质即可得出结论；②、根据①的过程可得出结论；
（2）根据题意画出图形，再根据平行线的性质即可得出∠EMB、∠END、∠MEN的关系．

解：（1）

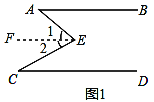
①如图1，过点E作EF∥AB，
∵AB∥CD，
∴AB∥CD∥EF，
∵∠A=45°，∠C=30°，
∴∠1=∠A=45°，∠2=∠C=30°，
∴∠AEC=∠1+∠2=75°；

②猜想： ．

理由：如图，过点作，

∵

∴（平行于同一条直线的两直线平行），

∴，（两直线平行，内错角相等），

∴（等量代换）；

（2）

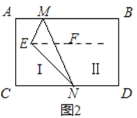
当点位于区域时， ，

理由：过E作EF∥AB，
∵AB∥CD，
∴AB∥CD∥EF，
∴∠BME+∠MEF=180°，∠DNE+∠NEF=180°，
∴∠EMB+∠END+∠MEN=360°；

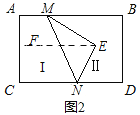
当点位于区域时， .

理由：过E作EF∥AB，
∵AB∥CD，
∴AB∥CD∥EF，
∴∠BMN=∠FEM，∠DNE=∠FEN，
∴∠EMB+∠END=∠MEF+∠NEF=∠MEN．

故答案为：（1）①，②，见解析；（2）当点位于区域时， ，当点位于区域时， .