题目内容
【题目】已知a、b满足![]() .请回管问题:
.请回管问题:
(1)请直接写出a、b的值,a=______,b=_______.
(2)当x的取值范围是_________时,![]() 有最小值,这个最小值是_____.
有最小值,这个最小值是_____.
(3)数轴a、b上两个数所对应的分别为A、B,AB的中点为点C,点A、B、C同时开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,点B和点C分别以每秒1个单位长度和3个单位长度的速度向右运动,当A、B两点重合时,运动停止.
①经过2秒后,求出点A与点B之间的距离AB.
②经过t秒后,请问:BC+AB的值是否随着时间t的变化而变化?若变化,请说明理由;若不变,请求其值.
【答案】(1)a=5,b=-1.(2) ![]() ,为6.(3)①2.②不变.
,为6.(3)①2.②不变.
【解析】
(1)根据非负数的性质,得到a-5=0,b+1=0,从而求出a,b的值;
(2)根据绝对值的几何意义,可得当表示x的点在表示a,b的点之间,则![]() 最小;
最小;
(3)①求出2秒后,A,B表示的数;
②用含有t的代数式分别表示BC,AB,再看看BC+AB的值与t是否相关.
解:(1)∵![]() ,
,
∴a-5=0,b+1=0,∴a=5,b=-1.
(2) 由(1)知,a=5,b=1,
根据绝对值的几何意义,可得当表示x的点在表示-1,5的点之间时,则![]() 最小为6,所以当-1≤x≤5 ,
最小为6,所以当-1≤x≤5 ,![]() 最小为6;
最小为6;
(3)①经过2秒后,点A运动的路程为1×2=2,则点A表示的数为5-2=3;
经过2秒后,点B运动的路程为1×2=2,则点B表示的数为-1+2=1;
所以AB之间的距离为3-1=2.
②运动ts后,AB=6-2t,BC=3+3t-t=3+2t,
∴AB+BC=6-2t+3+2t=9.
∴BC+AB的值与t是无关
(3)①经过2秒后,点A运动的路程为1×2=2,则点A表示的数为5-2=3;
经过2秒后,点B运动的路程为1×2=2,则点B表示的数为-1+2=1;
所以AB之间的距离为3-1=2.
②运动ts后,AB=6-2t,BC=3+3t-t=3+2t,
∴AB+BC=6-2t+3+2t=9.
∴BC+AB的值与t是无关.

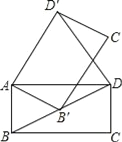
【题目】如图,在矩形ABCD中,AB=1,BC=![]() .将矩形ABCD绕点A逆时针旋转至矩形AB′C′D′,使得点B′恰好落在对角线BD上,连接DD′,则DD′的长度为( )
.将矩形ABCD绕点A逆时针旋转至矩形AB′C′D′,使得点B′恰好落在对角线BD上,连接DD′,则DD′的长度为( )
A. ![]() B.
B. ![]() C.
C. ![]() +1 D. 2
+1 D. 2
【题目】某检修小组从A地出发,在东西向的马路上检修线路,如果规定向东行驶为正,向西行驶为负,一天中七次行驶纪录如下.(单位:![]() )
)
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 |
|
|
|
|
|
|
|
(1)求收工时,检修小组在![]() 地的何方向?距离
地的何方向?距离![]() 地多远?
地多远?
(2)在第几次纪录时距![]() 地最远?
地最远?
(3)若汽车行驶每千米耗油0.4升,问从![]() 地出发,检修结束后再回到
地出发,检修结束后再回到![]() 地共耗油多少升?
地共耗油多少升?
【题目】已知二次函数![]() 的图象上部分点的横坐标x与纵坐标y的对应值如下表:
的图象上部分点的横坐标x与纵坐标y的对应值如下表:
x |
|
| 0 | 1 | 2 |
|
y |
| 0 | 3 | 4 | 3 |
|
那么关于它的图象,下列判断正确的是![]()
A. 开口向上 B. 与x轴的另一个交点是![]()
C. 与y轴交于负半轴 D. 在直线![]() 的左侧部分是下降的
的左侧部分是下降的