题目内容
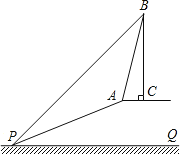
【题目】如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=24cm,BC=30cm.点P从点A出发,以1cm/s的速度向点D移动,点Q从点C出发,以3cm/s的速度向点B运动,点P和点Q分别从点A和点C同时出发,移动时间为ts.规定若其中一个动点先到达端点(终点)时,另一个动点也随之停止运动.
(1)求时间t的取值范围;
(2)当四边形ABQP为矩形时,求时间t的值;
(3)是否存在时间t的值,使得△APQ的面积是△ABC的面积的一半?若存在,请求出t的值,若不存在,说明理由.
【答案】
(1)解:点P停止的时间是24÷1=24s,点Q停止的时间是30÷3=10s,
所以时间t的取值范围是0≤t≤10
(2)解:由运动知,AP=t,CQ=3t,
∴BQ=30﹣3t,
若四边形ABQP是矩形.
∴AP=BQ.
即t=30﹣3t.
∴t=7.5.
(3)解:不存在.理由如下:
若△APQ的面积是△ABC的面积的一半时,
∴ ![]() AP×AB=
AP×AB= ![]() ×AB×BC.
×AB×BC.
∴t= ![]() ×30=15.
×30=15.
∵t的取值范围是0≤t≤10.
∴不存在t的值,使得使得△APQ的面积是△ABC的面积的一半.
【解析】(1)根据运动速度是距离即可得出结论;(2)有矩形的性质得出AP=BQ,建立方程求解即可得出结论;(3)假设△APQ的面积是△ABC的面积的一半,求出时间,判断是否在0≤t≤10内,即可得出结论.
【考点精析】解答此题的关键在于理解三角形的面积的相关知识,掌握三角形的面积=1/2×底×高,以及对矩形的性质的理解,了解矩形的四个角都是直角,矩形的对角线相等.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目