题目内容
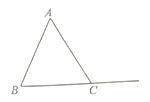
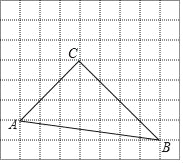
【题目】如图,在每个小正方形的边长为1的网格中,△ABC的顶点A,B,C均在格点上.
(1)∠ACB的大小为 (度)
(2)在如图所示的网格中,以A为中心,取旋转角等于∠BAC,把△ABC逆时针旋转,请用无刻度的直尺,画出旋转后的△ABC,并简要说明旋转后点C和点B的对应点点C′和点B′的位置是如何而找到的(不要求证明)
【答案】(1)90(2)见解析
【解析】
(1)利用勾股定理的逆定理即可解决问题.
(2)如图,延长AC到格点B′,使得AB′=AB=5![]() ,延长BC到格点E,连接AE,取格点F,连接FB′交AE于点C′,△AB′C′即为所求.
,延长BC到格点E,连接AE,取格点F,连接FB′交AE于点C′,△AB′C′即为所求.
(1)∵AC=3![]() ,BC=4
,BC=4![]() ,AB=5
,AB=5![]() ,
,
∴AB2=AC2+BC2,
∴∠ACB=90°,
故答案为90;
(2)如图,
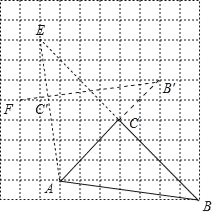
延长AC到格点B′,使得AB′=AB=5![]() ,延长BC到格点E,连接AE,取格点F,连接FB′交AE于点C′,△AB′C′即为所求.
,延长BC到格点E,连接AE,取格点F,连接FB′交AE于点C′,△AB′C′即为所求.

 一线名师提优试卷系列答案
一线名师提优试卷系列答案【题目】某企业为了解饮料自动售卖机的销售情况,对甲、乙两个城市的饮料自动售卖机进行抽样调查,从两个城市中所有的饮料自动售卖机中分别抽取16台,记录下某一天各自的销售情况(单位:元)如下:
甲:25、45、38、22、10、28、61、18、38、45、78、45、58、32、16、78
乙:48、52、21、25、33、12、42、39、41、42、33、44、33、18、68、72
整理、描述数据:对销售金额进行分组,各组的频数如下:
销传金额 |
|
|
|
|
甲 | 3 | 6 | 4 | 3 |
乙 | 2 | 6 | a | b |
分析数据:两组样本数据的平均数、中位数如下表所示:
城市 | 中位数 | 平均数 | 众数 |
甲 | C | 39.8 | 45 |
乙 | 40 | 38.9 | d |
请根据以上信息,回答下列问题:
(1)填空:a=, b=, c=, d=.
(2)两个城市目前共有饮料自动售卖机4000台,估计日销售金额不低于40元的数量约为多少台?
(3)根据以上数据,你认为甲、乙哪个城市的饮料自动售卖机销售情况较好?请说明理由(一条理由即可).