题目内容
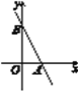
【题目】如图所示，在平面直角坐标系中，正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形，且相似比为1：3，点A，B，E在x轴上． 
（1）若点F的坐标为（6，3），直接写出点C和点A的坐标；
（2）若正方形BEFG的边长为6，求点C的坐标．
【答案】
（1）解：C点坐标为（2，1），A点坐标为（1，0）；
（2）解：∵正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形，
∴正方形BEFG的边长为6，则正方形ABCD的边长为2，OB：OE=1：3，
∴OB：（OB+6）=1：3，解得OB=3，
∴点C的坐标为（3，2）．
【解析】（1）利用关于原点为位似中心的对应点的坐标特征，把F点的横纵坐标都乘以 
即可得到C点坐标，然后利用正方形的性质写出A点坐标；（2）先利用位似的性质得到正方形ABCD的边长为2，再利用相似比求出OB，从而可得到C点坐标．
【考点精析】解答此题的关键在于理解正方形的性质的相关知识，掌握正方形四个角都是直角，四条边都相等；正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角；正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的对角线与边的夹角是45o；正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形，以及对位似变换的理解，了解它们具有相似图形的性质外还有图形的位置关系（每组对应点所在的直线都经过同一个点—位似中心）．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案【题目】某商场计划购进冰箱、彩电进行销售，已知冰箱的进货单价比彩电的进货单价多400元，若商场用80 000元购进冰箱的数量与用64 000元购进彩电的数量相等.该商场冰箱、彩电的售货单价如下表：
冰箱 | 彩电 | |
售价（元/台） | 2500 | 2000 |
（1）分别求出冰箱、彩电的进货单价.
（2）为了满足市场需求，商场决定用不超过90 000元的资金采购冰箱、彩电共50台。若该商场将购进的冰箱、彩电共50台全部售出，获得利润为w元，为了使商场的利润最大，该商场该如何购进冰箱、彩电，最大利润是多少？
【题目】某校九年级学生开展踢毽子比赛活动，每班派5名同学参加，按团体总分多少排列名次，在规定时间内每人踢100个以上(含100)为优秀，下表是成绩最好的甲班和乙班5名学生的比赛数据(单位：个)：
1号 | 2号 | 3号 | 4号 | 5号 | 总分 | |
甲班 | 100 | 98 | 110 | 89 | 103 | 500 |
乙班 | 89 | 100 | 95 | 119 | 97 | 500 |
统计发现两班总分相等，此时有同学建议，可以通过考查数据中的其他信息作为参考，请你解答下列问题：
(1)计算两班的优秀率；
(2)求两班比赛数据的中位数；
(3)估计两班比赛数据的方差哪一个小？
(4)根据以上三条信息，你认为应该把冠军奖状发给哪一个班？简述理由．
