题目内容
【题目】为了估计鱼塘中成品鱼(个体质量在0.5 kg及以上,下同)的总质量,先从鱼塘中捕捞50条成品鱼,称得它们的质量如下表:

然后做上记号再放回鱼塘中,过几天又捕捞了100条成品鱼,发现其中2条带有记号.
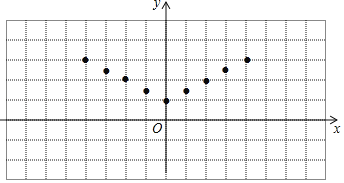
(1)请根据表中数据补全下面的直方图(各组中数据包括左端点不包括右端点);

(2)根据图中数据分组,估计从鱼塘中随机捕一条成品鱼,其质量落在哪一组的可能性最大?
(3)根据图中数据分组,估计鱼塘里质量中等的成品鱼,其质量落在哪一组内?
(4)请你用适当的方法估计鱼塘中成品鱼的总质量(精确到1 kg).
【答案】(1)补图略;(2)其质量落在0.5~0.8 kg这一组的可能性最大;(3)质量落在0.8~1.1 kg这一组内;(4)平均数2260kg.
【解析】(1)由函数图象可以得出1.1-1.4的有5条,补全图形,得

(2)由题意,得
0.5-0.8的频率为:24÷50=0.48,
0.8-1.1的频率为:18÷50=0.36,
1.1-1.4的频率为:5÷50=0.1,
1.4-1.7的频率为:1÷50=0.02,
1.7-2.0的频率为:2÷50=0.04.
∵0.48>0.36>0.1>0.04>0.02.
∴估计从鱼塘中随机捕一条成品鱼,其质量落在0.5-0.8 kg的可能性最大.
(3)这组数据的个数为50,就可以得出第25个和第26个数分别是1.0,1.0,
∴(1.0+1.0)÷2=1.0
∴鱼塘里质量中等的成品鱼,其质量落在0.8-1.1 kg内;
(4)设鱼塘中成品鱼的总质量为x,由题意,得
50:x=2:100,解得:x=2500.
∵2500×0.5×1+0.6×8+0.7×15+1×18+1.2×5+1.6×1×2500.5×1+0.6×8+0.7×15+1×18+1.2×5+1.6×1×250=2260,
∴估计鱼塘中成品鱼的总质量为2260kg.
分析:(1)由函数图象可以得出1.1-1.4的有5条,就可以补全直方图;
(2)分别求出各组的频率,就可以得出结论;
(3)由这组数据的个数为50,就可以得出第25个和第26个数的平均数就可以得出结论;
(4)设鱼塘中成品鱼的条数为x,根据作记号的鱼50:x=2:100建立方程求出其解即可.
详解:(1)由函数图象可以得出1.1-1.4的有5条,补全图形,得:
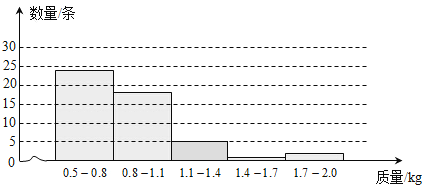
(2)由题意,得
0.5-0.8的频率为:24÷50=0.48,
0.8-1.1的频率为:18÷50=0.36,
1.1-1.4的频率为:5÷50=0.1,
1.4-1.7的频率为:1÷50=0.02,
1.7-2.0的频率为:2÷50=0.04.
∵0.48>0.36>0.1>0.04>0.02.
∴估计从鱼塘中随机捕一条成品鱼,其质量落在0.5-0.8的可能性最大;
(3)这组数据的个数为50,就可以得出第25个和第26个数分别是1.0,1.0,
∴(1.0+1.0)÷2=1.0,
鱼塘里质量中等的成品鱼,其质量落在0.8-1.1内;
(4)设鱼塘中成品鱼的条数为x,由题意,得:
50:x=2:100,
解得:x=2500.
2500×0.5×1+0.6×8+0.7×15+1×18+1.2×5+1.6×1×2500.5×1+0.6×8+0.7×15+1×18+1.2×5+1.6×1×250=2260kg.

【题目】某校数学兴趣小组根据学习函数的经验,对函数y=![]() |x|+1的图象和性质进行了探究,探究过程如下:(1)自变量x的取值范围是全体实数,x与y的几组对应值如表:
|x|+1的图象和性质进行了探究,探究过程如下:(1)自变量x的取值范围是全体实数,x与y的几组对应值如表:
X | … | ﹣4 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | … |
Y | … | 3 | 2.5 | m | 1.5 | 1 | 1.5 | 2 | 2.5 | 3 | … |
(1)其中m= .
(2)如图,在平面直角坐标系xOy中,描出了上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(3)当2<y≤3时,x的取值范围为 .