题目内容
【题目】某校数学兴趣小组根据学习函数的经验,对函数y=![]() |x|+1的图象和性质进行了探究,探究过程如下:(1)自变量x的取值范围是全体实数,x与y的几组对应值如表:
|x|+1的图象和性质进行了探究,探究过程如下:(1)自变量x的取值范围是全体实数,x与y的几组对应值如表:
X | … | ﹣4 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | … |
Y | … | 3 | 2.5 | m | 1.5 | 1 | 1.5 | 2 | 2.5 | 3 | … |
(1)其中m= .
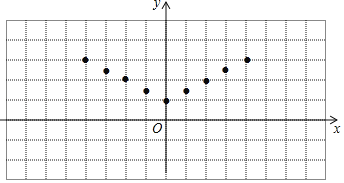
(2)如图,在平面直角坐标系xOy中,描出了上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(3)当2<y≤3时,x的取值范围为 .
【答案】(1)2;(2)见解析;(3)﹣4≤x<﹣2或2<x≤4
【解析】
(1)依据在y=![]() |x|+1中,令x=﹣2,则y=2,可得m的值;
|x|+1中,令x=﹣2,则y=2,可得m的值;
(2)将图中的各点用平滑的曲线连接,即可画出该函数的图象;
(3)依据函数图象,即可得到当2<y≤3时,x的取值范围.
(1)在y=![]() |x|+1中,令x=﹣2,则y=2,
|x|+1中,令x=﹣2,则y=2,
∴m=2,
故答案为:2;
(2)如图所示:
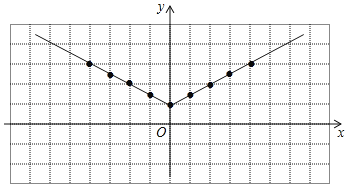
(3)由图可得,当2<y≤3时,x的取值范围为﹣4≤x<﹣2或2<x≤4.
故答案为:﹣4≤x<﹣2或2<x≤4.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目