题目内容
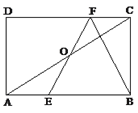
【题目】如图1,正方形ABCD中,点E、F分别在边DC、AD上,且AE⊥BF于G. 
(1)求证:BF=AE;
(2)如图2,当点E在DC延长线上,点F在AD延长线上时,(1)中结论是否成立?(直接写结论) 
(3)在图2中,若点M、N、P、Q分别为四边形AFEB四条边AF、EF、EB、AB的中点,且AF:AD=4:3,求S四边形MNPQ:S正方形ABCD .
【答案】
(1)
解:∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠DAB=∠ADC=90°.
∴∠DAE+∠BAE=90°.
∵AE⊥BF,
∴∠AGB=90°,
∴∠GAB+∠GBA=90°,
∴∠DAE=∠ABG.
在△ABF和△DAE中,
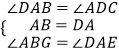 ,
,
∴△ABF≌△DAE(ASA),
∴BF=AE;
(2)
解:)结论成立 即AE=BF.
理由:∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠DAB=∠ADC=90°.
∴∠DAE+∠BAE=90°.
∵AE⊥BF,
∴∠AGB=90°,
∴∠GAB+∠GBA=90°,
∴∠DAE=∠ABG.
在△ABF和△DAE中,
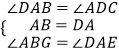 ,
,
∴△ABF≌△DAE(ASA),
∴BF=AE;
(3)
解:∵AF:AD=4:3,设AF=4a,AD=3a,
∴DF=a.
∵△ABF≌△DAE,
∴AF=DE,
∴AF﹣AD=DE﹣DC,
∴DF=CE,
∴CE=a.
∵点M、N、P、Q分别为四边形AFEB四条边AF、EF、EB、AB的中点,
∴MN是△AEF的中位线,MQ是△ABF的中位线,
∴MN= ![]() AE,MN∥AE,MQ=
AE,MN∥AE,MQ= ![]() BF,MQ∥BF.
BF,MQ∥BF.
∴MN=MQ.∠MNP=∠NPQ=∠PQM=90°,
∴四边形MNPQ是正方形.
在Rt△ABF中,由勾股定理,得
BF=5a.
∴MN=MQ= ![]() .
.
∴S四边形MNPQ= ![]() .
.
∵S正方形ABCD=9a2,
∴S四边形MNPQ:S正方形ABCD= ![]() :9a2=25:36.
:9a2=25:36.
答:S四边形MNPQ:S正方形ABCD=25:36.
【解析】(1)根据正方形的性质就可以求出△ABF≌△DAE,就可以得出结论;(2)根据正方形的性质就可以求出△ABF≌△DAE就可以得出BF=AE;(3)根据条件可以设AF=4a,AD=3a,就可以求出DF=CE=a,由勾股定理就可以求出AE,由中位线的性质就可以求出MN的值,表示出正方形MNPQ的面积,就可以求出结论.
【考点精析】认真审题,首先需要了解正方形的性质(正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形).

【题目】小明统计了他家今年5月份打电话的次数及通话时间,并列出了频数分布表:
通话时间x/分钟 | 0<x≤5 | 5<x≤10 | 10<x≤15 | 15<x≤20 |
频数(通话次数) | 20 | 16 | 9 | 5 |
则5月份通话次数中,通话时间不超过15分钟的所占百分比是( )
A. 10% B. 40% C. 50% D. 90%