题目内容
【题目】定义: 在平面直角坐标系中,如果点![]() 和
和![]() 都在某函数的图象
都在某函数的图象![]() 上,则称点
上,则称点![]() 是图象
是图象![]() 的一对“相关点”.例如,点
的一对“相关点”.例如,点![]() 和点
和点![]() 是直线
是直线![]() 的一对相关点.
的一对相关点.
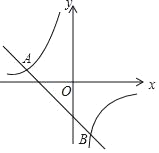
![]() 请写出反比例函数
请写出反比例函数![]() 的图象上的一对相关点的坐标;
的图象上的一对相关点的坐标;
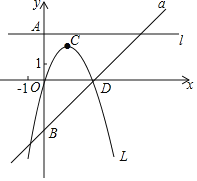
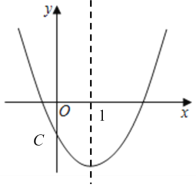
![]() 如图,抛物线
如图,抛物线![]() 的对称轴为直线
的对称轴为直线![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
![]() 求抛物线的解析式:
求抛物线的解析式:
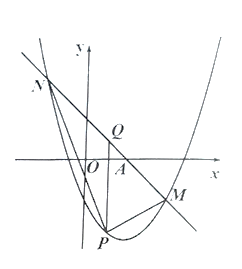
![]() 若点
若点![]() 是抛物线
是抛物线![]() 上的一对相关点,直线
上的一对相关点,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,点
,点![]() 为抛物线
为抛物线![]() 上之间的一点,求
上之间的一点,求![]() 面积的最大值.
面积的最大值.
【答案】(1)![]() ,
,![]() ;(2)①
;(2)①![]() ;②
;②![]()
【解析】
(1)xy=6,当x=2时,y=3,当x=3时,y=2,即可求解;
(2)①根据C(0,-1)求得c,根据x=-1,函数对称轴为:x=-![]() =-1,解得:b=-2,即可求解;
=-1,解得:b=-2,即可求解;
②由“相关点”的定义,可得直线MN的表达式,求出点M、N的坐标,将△PMN面积利用S=![]() ×PQ×(xM-xN)表示出来即可求解.
×PQ×(xM-xN)表示出来即可求解.
解:(1)xy=6,当x=2时,y=3,当x=3时,y=2,
故答案为:(2,3)和(3,2);
(2)①∵抛物线![]() 的对称轴为直线
的对称轴为直线![]() ,
,
![]() 解得
解得![]() ,
,
![]() 抛物线
抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,
![]() ,
,
![]() 抛物线的解析式为
抛物线的解析式为![]() ;
;
②由相关点定义得,点![]() 关于直线
关于直线![]() 对称.
对称.
又![]() 直线
直线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,
![]() 直线
直线![]() 的解析式为
的解析式为![]() .
.
代入抛物线的解析式![]() 中,并整理,得
中,并整理,得
![]() ,
,
解得,![]() ,
,![]()
![]() 两点坐标为
两点坐标为![]() 和
和![]() .
.
设点![]() 的横坐标为
的横坐标为![]() ,则点
,则点![]() ,
,
过![]() 作
作![]() 轴交直线
轴交直线![]() 于
于![]() 点,
点,
则![]() 点坐标为
点坐标为![]() ,
,
![]()
![]()
![]() ,
,
即当![]() 时,
时,![]() 的面积最大,最大值为
的面积最大,最大值为![]() .
.

 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案 名题金卷系列答案
名题金卷系列答案【题目】为了了解某小区青年对“高铁”、“扫码支付”、“网购”和“共享单车”新四大发明的喜爱程度,随机调查该小区一部分青年(每名青年只能选一个),并将调查结果制成如图所示统计表与条形统计图.
青年最喜爱的新四大发明人数统计表
节目 | 人数(名) | 百分比 |
共享单车 | 5 |
|
扫码支付 | 15 |
|
网购 |
|
|
高铁 | 10 |
|
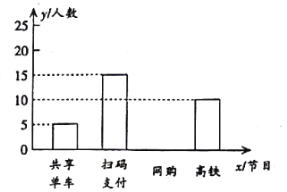
青年最喜爱的新四大发明人数条形统计图
(1)计算![]() 的值
的值![]() ;
;
(2)请补全条形统计图;
(3)在被调查喜爱“共享单车”青年中,小明一周内使用共享单车的次数分别为:1,3,5,12,![]() ,若整数
,若整数![]() 是这组数据的中位数,直接写出该组数据的平均数.
是这组数据的中位数,直接写出该组数据的平均数.