Question

【题目】在平面直角坐标系中，矩形OABC的顶点B的坐标为（2，4），抛物线y=-2x2+bx+c经过A、C两点，与x轴的另一个交点为点D．

（1）如图1，求抛物线的函数表达式；

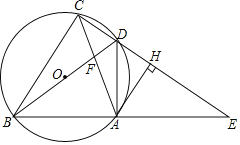
（2）如图2，连接AC、AD，将△ABC沿AC折叠后与AD、y轴分别交于点交于E、G，求OG的长度；

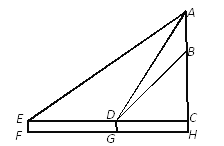
（3）如图3，将抛物线在AC上方的图象沿AC折叠后与y轴交与点F，求点F的坐标．

Answer 1

【答案】（1）y=-2x2+2x+4；（2）；（3）F（0，）．

【解析】

（1）先根据四边形ABCD是矩形得出点A．C坐标，再代入解析式求出b．c的值，从而得出答案；

（2）由△ABC≌△AB′C知∠BCA=∠B′CA．由AO∥BC知∠BCA=∠B′CA，∠BCA=∠OAC，从而得∠B′CA=∠OAC．据此知AG=CG．设OG=x，则AG=CG=4-x．在Rt△OGC中，利用勾股定理可以求得x的值；

（3）在AC上方的抛物线图象取点F的对称点F′，过点F′作y轴的平行线交直线AC于点G，先证F′A=F′G，继而得直线AC的解析式为y=-2x+4，设点F（n，-2n2+2n+4），则G（n，-2n+4）．根据F′A2=F′G2求出n的值，从而得出，F′A=F′G=FA=，从而得出点F的坐标．

解：（1）如图1，

∵四边形OABC是矩形，B（2，4），

∴A（0，4），C（2，0），

∵抛物线y=-2x2+bx+c经过A．C两点，

∴，

∴，

∴抛物线的函数表达式为：y=-2x2+2x+4；

（2）如图2，

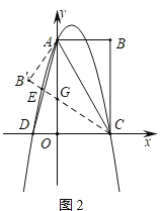
由题意得：△ABC≌△AB′C．

∴∠BCA=∠B′CA．

∵AO∥BC，

∴∠BCA=∠B′CA，∠BCA=∠OAC，

∴∠B′CA=∠OAC．

∴AG=CG．

设OG=x，则AG=CG=4-x．

在Rt△OGC中，22+x2=（4-x）2，

得，

∴；

（3）如图3，在AC上方的抛物线图象取点F的对称点F′，过点F′作y轴的平行线交直线AC于点G．

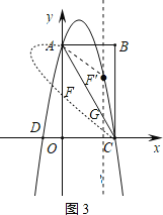
由题意得：∠FAC=∠F′AC，F′A=FA．

∵AO∥F′G，

∴∠FAC=∠AGF′．

∵∠FAC=∠F′AC，∠FAC=∠AGF′．

∴∠F′AC=∠AGF′，

∴F′A=F′G．

设直线AC的解析式为y=kx+b，

把A（0，4），C（2，0）代入得，解得

∴直线AC的解析式为：y=-2x+4．

设点F（n，-2n2+2n+4），则G（n，-2n+4）．

∴F′G=-2n2+4n，F′A2=n2+（-2n2+2n）2．

∵F′A=F′G．

∴F′A2=F′G2．

即：n2+（-2n2+4n）2=（-2n2+2n）2，

解得：n1=0（舍去），．

∴．

∴F′A=F′G=FA=，

∴F（0，）．