题目内容
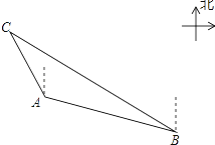
【题目】如图,一艘海上巡逻船在A地巡航,这时接到B地海上指挥中心紧急通知:在指挥中心北偏西60°方向的C地有一艘渔船遇险,要求马上前去救援,要求马上前去救援.此时C地位于A地北偏西30°方向上,A地位于B地北偏西75°方向上,A、B两地之间的距离为12海里,则A、C两地之间的距离为________.
【答案】(6![]() ﹣6
﹣6![]() )(海里)
)(海里)
【解析】
过点B作BD⊥CA交CA延长线于点D,根据题意可得∠ACB和∠ABC的度数,然后根据三角形外角定理求出∠DAB的度数,已知AB=12海里,可求出BD、AD的长度,在Rt△CBD中,解直角三角形求出CD的长度,继而可求出A、C之间的距离.
过点B作BD⊥CA交CA延长线于点D,
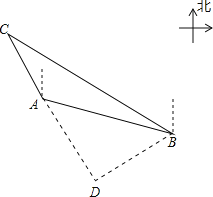
由题意得,∠ACB=60°-30°=30°,
∠ABC=75°-60°=15°,
∴∠DAB=∠DBA=45°,
在Rt△ABD中,AB=12,∠DAB=45°,
∴BD=AD=ABcos45°=6![]() ,
,
在Rt△CBD中,CD=![]() =6
=6![]() ,
,
∴AC=(6![]() -6
-6![]() )(海里),
)(海里),
故答案为:(6![]() -6
-6![]() )(海里).
)(海里).

练习册系列答案
相关题目