Question

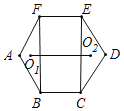
【题目】如图，正六边形ABCDEF的边长是6+4，点O1，O2分别是△ABF，△CDE的内心，则O1O2=_____．

Answer 1

【答案】9+4

【解析】如图，设△AFB的内切圆的半径为r，过A作AM⊥BF于M，连接O1F、O1A、O1B，解直角三角形求出AM、FM、BM，根据三角形的面积求出r，即可求出答案．

如图，过A作AM⊥BF于M，连接O1F、O1A、O1B，

∵六边形ABCDEF是正六边形，

∴∠A==120°，AF=AB，

∴∠AFB=∠ABF=×（180°﹣120°）=30°，

∴△AFB边BF上的高AM=AF=×（6+4）=3+2，

FM=BM=AM=3+6，

∴BF=3+6+3+6=12+6，

设△AFB的内切圆的半径为r，

∵S△AFB=，

∴×（3+2）×（3+6）

=×（6+4）×r+×（6+4）×r+×（12+6）×r，

解得：r=，

即O1M=r=，

∴O1O2=2×+6+4=9+4，

故答案为：9+4．