题目内容
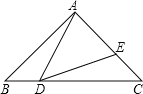
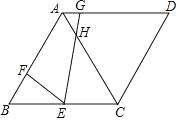
【题目】如图,在菱形ABCD中,∠B=60°,BC=6,E为BC中点,F是AB上一点,G为AD上一点,且BF=2,∠FEG=60°,EG交AC于点H,下列结论:①△BEF∽△CHE;②AG=1;③EH=![]() ;④S△BEF=3S△AGH;正确的是______.(填序号即可)
;④S△BEF=3S△AGH;正确的是______.(填序号即可)
【答案】①②③
【解析】
①菱形的性质以及一线三等角即可证明△BEF∽△CHE,故①正确;
②由△BEF∽△CHE,可得![]() ,从而求得CH,由此可得AH,由△AGH∽△CEH,可得
,从而求得CH,由此可得AH,由△AGH∽△CEH,可得![]() ,从而求得AH=1,故②正确;
,从而求得AH=1,故②正确;
③过H作HM⊥BC于点M,在Rt△HMC中,HM=HC·sin60![]() ,MC=HC·sin30=
,MC=HC·sin30=![]() ,可得ME=EC-MC=
,可得ME=EC-MC=![]() ,在Rt△MEH中,由勾股定理可得EH=
,在Rt△MEH中,由勾股定理可得EH=![]() ,故③正确;
,故③正确;
④由△BEF∽△CHE,△AHG∽△CHE,可得△BEF∽△AHG,即![]() ,即S△BEF=4S△AGH,故④错误,故答案为:①②③
,即S△BEF=4S△AGH,故④错误,故答案为:①②③
①∵四边形ABCD是菱形,∠B=60 ,BC=6,
∴AB=BC=AC=6,
∵∠CEH+∠FEH+∠FEB=180 ,∠B+∠FEB+∠BFE=180 ,∠B=∠FEH =60 ,
∴∠BFE=∠CEH,
∴△BEF∽△CHE,故①正确;
②∵E是BC的中点,
∴BE=CE=3,
∵△BEF∽△CHE,
∴![]() ,即
,即![]() ,
,
∴CH=![]() ,
,
∴AH=AC-CH=6-![]() =
=![]() ,
,
∵AD∥BC,
∴△AGH∽△CEH,
∴![]() ,即
,即![]() ,
,
∴AH=1,故②正确;
③过H作HM⊥BC于点M,
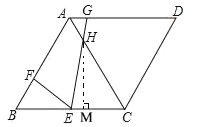
在Rt△HMC中,∠C=60,HC=![]() ,
,
∴HM=HC·sin60=![]() ,
,
MC=HC·sin30=![]() ,
,
∴ME=EC-MC=3-![]() =
=![]() ,
,
在Rt△MEH中,HE=![]() =
=![]() ,故③正确;
,故③正确;
④∵△BEF∽△CHE,△AHG∽△CHE,
∴△BEF∽△AHG,
∴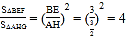 ,
,
即S△BEF=4S△AGH,故④错误,
故答案为:①②③

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目