题目内容
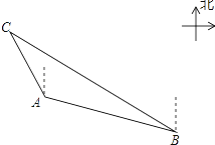
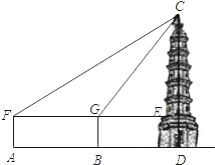
【题目】在一次数学活动课上,老师带领同学们去测量一座古塔CD的高度.他们首先从A处安置测倾器,测得塔顶C的仰角∠CFE=21°,然后往塔的方向前进50米到达B处,此时测得仰角∠CGE=37°,已知测倾器高1.5米,请你根据以上数据计算出古塔CD的高度.
(参考数据:sin37° ![]() ,tan37°
,tan37° ![]() ,sin21°≈
,sin21°≈![]() ,tan21°≈
,tan21°≈![]() )
)
【答案】古塔的高度约是39米.
【解析】
首先分析图形,根据题意构造直角三角形.本题涉及到两个直角三角形△CEF、△CGE,利用其公共边CE构造等量关系,借助FG=EF﹣GE=50,构造方程关系式求解.
由题意知CD⊥AD,EF∥AD.
∴∠CEF=90°.
设CE=x,
在Rt△CEF中,
tan∠CFE= ![]() ,
,
则EF= ![]() x.
x.
在Rt△CEG中,
tan∠CGE= ![]() ,
,
则GE= ![]() .
.
∵EF=FG+EG,
∴ ![]() x,
x,
x=37.5.
∴CD=CE+ED=37.5+1.5=39(米).
答:古塔的高度约是39米.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
相关题目