题目内容
如图,在菱形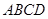 中,
中,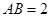 ,
,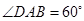 ,点
,点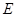 是
是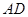 边的中点,点
边的中点,点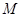 是
是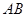 边上一动点(不与点
边上一动点(不与点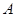 重合),延长
重合),延长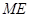 交射线
交射线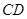 于点
于点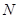 ,连接
,连接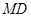 ,
,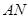 .
.
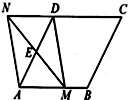
(1)求证:四边形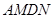 是平行四边形;
是平行四边形;
(2)填空:①当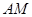 的值为 时,四边形
的值为 时,四边形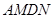 是矩形;
是矩形;
②当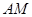 的值为 时,四边形
的值为 时,四边形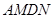 是菱形.
是菱形.
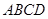 中,
中,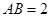 ,
,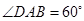 ,点
,点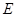 是
是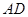 边的中点,点
边的中点,点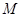 是
是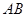 边上一动点(不与点
边上一动点(不与点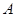 重合),延长
重合),延长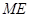 交射线
交射线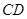 于点
于点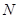 ,连接
,连接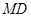 ,
,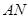 .
.
(1)求证:四边形
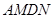 是平行四边形;
是平行四边形;(2)填空:①当
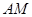 的值为 时,四边形
的值为 时,四边形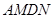 是矩形;
是矩形;②当
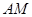 的值为 时,四边形
的值为 时,四边形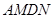 是菱形.
是菱形.(1)根据菱形的性质可得ND∥AM,即可证得 ,再根据中点的性质可得DE=AE,即可证得△NDE≌△MAE,从而可证得结论;(2)①1 ;②2
,再根据中点的性质可得DE=AE,即可证得△NDE≌△MAE,从而可证得结论;(2)①1 ;②2
 ,再根据中点的性质可得DE=AE,即可证得△NDE≌△MAE,从而可证得结论;(2)①1 ;②2
,再根据中点的性质可得DE=AE,即可证得△NDE≌△MAE,从而可证得结论;(2)①1 ;②2 试题分析:(1)根据菱形的性质可得ND∥AM,即可证得
 ,再根据中点的性质可得DE=AE,即可证得△NDE≌△MAE,从而可证得结论;
,再根据中点的性质可得DE=AE,即可证得△NDE≌△MAE,从而可证得结论;(2)根据矩形、菱形的判定方法结合图形特征即可求得结果.
(1)∵四边形ABCD是菱形,
∴ND∥AM
∴

又∵点E是AD中点,
∴DE=AE
∴△NDE≌△MAE
∴ND=MA
∴四边形
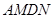 是平行四边形;
是平行四边形;(2)①当
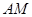 的值为1时,四边形
的值为1时,四边形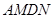 是矩形;
是矩形;②当
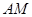 的值为2时,四边形
的值为2时,四边形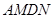 是菱形.
是菱形.点评:特殊四边形的判定和性质是初中数学的重点,贯穿于整个初中数学的学习,是中考中比较常见的知识点,一般难度不大,需熟练掌握.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目

 ABCD的两条对角线AC、BD相交于点
ABCD的两条对角线AC、BD相交于点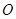 ,
,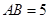 ,
,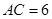 ,
,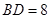 ,则
,则
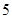 B.
B.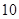 C.
C.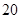 D.
D.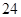

 ,则BN的长是 ,
,则BN的长是 , 的值等于 ;若
的值等于 ;若 (
( ,且
,且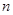 为整数),则
为整数),则


 的值.
的值.