题目内容
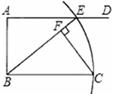
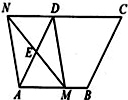
如图,将边长为2的正方形纸片ABCD折叠,使点B 落在CD上,落点记为E(不与点C,D重合),点A落在点F处,折痕MN交AD于点M,交BC于点N.若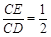 ,则BN的长是 ,
,则BN的长是 ,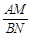 的值等于 ;若
的值等于 ;若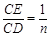 (
( ,且
,且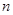 为整数),则
为整数),则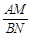 的值等于 (用含
的值等于 (用含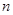 的式子表示).
的式子表示).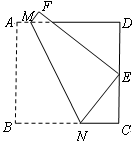
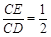 ,则BN的长是 ,
,则BN的长是 ,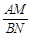 的值等于 ;若
的值等于 ;若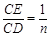 (
( ,且
,且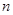 为整数),则
为整数),则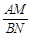 的值等于 (用含
的值等于 (用含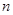 的式子表示).
的式子表示).
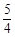 ,
,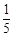 ,
,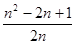
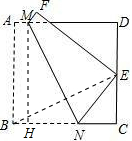
试题分析:连接BM,EM,BE,由题设,得四边形ABNM和四边形FENM关于直线MN对称,即可到得MN垂直平分BE,则BM=EM,BN=EN.根据正方形的性质可得∠A=∠D=∠C=90°,设AB=BC=CD=DA=2,由
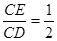 可得CE=DE=1,设BN=x,则NE=x,NC=2-x,在Rt△CNE中,根据勾股定理即可列方程求得x的值,从而得到BN的长,在Rt△ABM和在Rt△DEM中,根据勾股定理可得AM2+AB2=BM2,DM2+DE2=EM2,则AM2+AB2=DM2+DE2.设AM=y,则DM=2-y,
可得CE=DE=1,设BN=x,则NE=x,NC=2-x,在Rt△CNE中,根据勾股定理即可列方程求得x的值,从而得到BN的长,在Rt△ABM和在Rt△DEM中,根据勾股定理可得AM2+AB2=BM2,DM2+DE2=EM2,则AM2+AB2=DM2+DE2.设AM=y,则DM=2-y,即可列方程求得
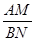 的值;当四边形ABCD为正方形时,连接BE,
的值;当四边形ABCD为正方形时,连接BE,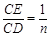 ,不妨令CD=CB=n,则CE=1,设BN=x,则EN=x,EN2=NC2+CE2,x2=(n-x)2+12,x=
,不妨令CD=CB=n,则CE=1,设BN=x,则EN=x,EN2=NC2+CE2,x2=(n-x)2+12,x=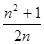 ;作MH⊥BC于H,则MH=BC,又点B,E关于MN对称,则MN⊥BE,∠EBC+∠BNM=90°;而∠NMH+∠BNM=90°,故∠EBC=∠NMH,则△EBC≌△NMH,则NH=EC=1,AM=BH=BN-NH=
;作MH⊥BC于H,则MH=BC,又点B,E关于MN对称,则MN⊥BE,∠EBC+∠BNM=90°;而∠NMH+∠BNM=90°,故∠EBC=∠NMH,则△EBC≌△NMH,则NH=EC=1,AM=BH=BN-NH=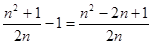 ,从而可以求得结果.
,从而可以求得结果.连接BM,EM,BE
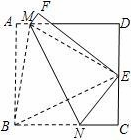
由题设,得四边形ABNM和四边形FENM关于直线MN对称.
∴MN垂直平分BE,
∴BM=EM,BN=EN.
∵四边形ABCD是正方形,
∴∠A=∠D=∠C=90°,设AB=BC=CD=DA=2.
∵
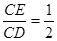 ,
,∴CE=DE=1.
设BN=x,则NE=x,NC=2-x.
在Rt△CNE中,NE2=CN2+CE2.
∴x2=(2-x)2+12,
解得
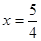 ,即
,即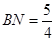
在Rt△ABM和在Rt△DEM中,AM2+AB2=BM2,DM2+DE2=EM2,
∴AM2+AB2=DM2+DE2.
设AM=y,则DM=2-y,
∴y2+22=(2-y)2+12,
解得
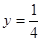 ,即
,即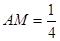
∴
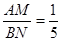
当四边形ABCD为正方形时,连接BE,
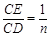 ,
,不妨令CD=CB=n,则CE=1,设BN=x,则EN=x,EN2=NC2+CE2,x2=(n-x)2+12,x=
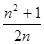 ;
;作MH⊥BC于H,则MH=BC,
又点B,E关于MN对称,则MN⊥BE,∠EBC+∠BNM=90°;
而∠NMH+∠BNM=90°,故∠EBC=∠NMH,则△EBC≌△NMH,
∴NH=EC=1,AM=BH=BN-NH=
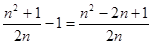
则:
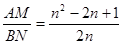 .
.点评:折叠的性质:折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
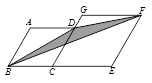
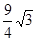
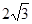
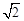
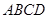 中,
中,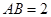 ,
,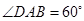 ,点
,点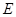 是
是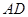 边的中点,点
边的中点,点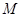 是
是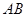 边上一动点(不与点
边上一动点(不与点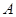 重合),延长
重合),延长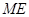 交射线
交射线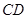 于点
于点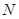 ,连接
,连接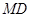 ,
,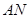 .
.
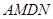 是平行四边形;
是平行四边形;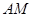 的值为 时,四边形
的值为 时,四边形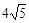 ,DB="4," 求四边形ABCD的面积.
,DB="4," 求四边形ABCD的面积.