��Ŀ����
����Ŀ����ͼ��a�������ABCDE���Ŵ�үʮ��ǰ�а���һ������ʾ��ͼ���������꿪�ѻĵأ����Ѿ����ͼ��b����ʾ����״.���а������뿪�ѻĵصķֽ�С·����ͼ��b��������CDE��������.�Ŵ�ү���E����һ��ֱ·EF��ֱ·�ú�Ҫ����ֱ·��ߵ����������а�ʱ��һ���࣬�ұߵ���������뿪�ѵĻĵ����һ����.�����Ʒֽ�С·��ֱ·��ռ��������������й�֪ʶ�����Ŵ�ү����·Ҫ����ͼ��b���л�����Ӧ��ͼ�Σ�����ر�����ͼ�ۼ���.
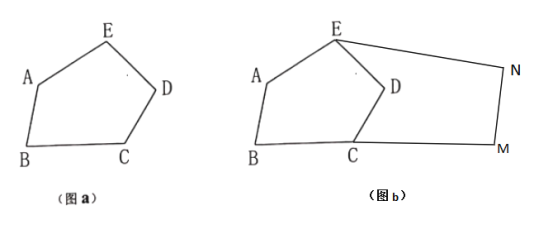
���𰸡�������.
��������
Ҫ�����������Ҫ������E�����ǿ��Լ�����һֱ���Ѿ��������۲���Է��֣�ʵ�����ǽ���EDC���еȻ��任����ʱֻҪ����EC�����ó߹���ͼ����D��EC��ƽ���ߣ���EN�ڵ�F����CM�ڵ�G��������EG��������ƽ����ľ��봦����ȣ��ɵ�S��ECG=S��ECD�����⼴�ý��.
�⣺������ͼ1��ʾ������EC����EDΪһ������EDF=��DEC����
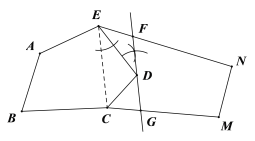

ͼ1 ͼ2
��ͼ2������EG������ͼ֪��EDF=��DEC������DF��EC����ֱ��DF��EN�ڵ�F����CM�ڵ�G�����߶�EG��Ϊ����ֱ·��λ��.
�������£���ͼ2��
��EC��FG��
��D��G�㵽EC�ľ�����ȣ�ƽ����ľ��봦����ȣ���
�֡�ECΪ�����ߣ�
��S��ECG=S��ECD��ͬ�ȸߵ��������������ȣ���
��S�����AEDCB= S�ı���ABCE+S��ECD=S�ı���ABCE+ S��ECG��S�����EDCMN=S�ı���EGMN��
��EFΪֱ·��λ�ã����Ա���ֱ·��ߵ����������а�ʱ��һ���࣬�ұߵ���������뿪�ѵĻĵ����һ����.