Question

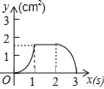
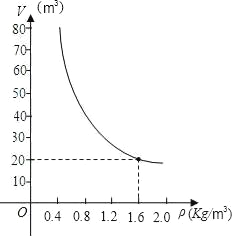
【题目】已知质量一定的某物体的体积V（m3）是密度ρ（kg/m3）的反比例函数，其图象如图所示：

（1）请写出该物体的体积V与密度ρ的函数关系式；

（2）当该物体的密度ρ=3.2Kg/m3时，它的体积v是多少？

（3）如果将该物体的体积控制在10m3～40m3之间，那么该物体的密度应在什么范围内变化？

Answer 1

【答案】（1）V=；（2）10（m）3；（3）该物体的密度在0.8Kg/m3～3.2Kg/m3的范围内变化．

【解析】【试题分析】

（1）用待定系数法求解析式，设V=，根据题意，当ρ=1.6时，v=20，

即k=ρV=20×1.6=32．得V=．

（2）直接代入解析式，即可.当=3.2时，V==10（m）3．

（3）当V=40时， =40，∴ρ=0.8（Kg/m3）．由（2）知V=10时，ρ=3.2

即该物体的体积在10m3～40m3时，该物体的密度在0.8Kg/m3～3.2Kg/m3的范围内变化．

【试题解析】

（1）设V=，

∵ρ=1.6时，v=20，

∴k=ρV=20×1.6=32．

∴V=．

（2）当P=3.2时，V==10（m）3．

（3）当V=40时， =40，∴ρ=0.8（Kg/m3）．

由（2）知V=10时，ρ=3.2

即该物体的体积在10m3～40m3时，

该物体的密度在0.8Kg/m3～3.2Kg/m3的范围内变化．