题目内容
已知⊙O的半径为6cm，P是⊙O内一点，OP=2cm，那么过P的最短的弦长等于分析：过P的最长的弦是过点P的直径，过P的最短的弦是与这条直径垂直的弦，画出图形，根据勾股定理和垂径定理求解即可．
解答：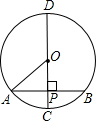
解：如图，
∵OA=6cm，OP=2cm，∴由勾股定理得，AP=4
cm，
∴AB=8
cm，
∴过P的最短的弦长等于8
cm，
故答案为8
；12．
解：如图，∵OA=6cm，OP=2cm，∴由勾股定理得，AP=4
| 2 |
∴AB=8
| 2 |
∴过P的最短的弦长等于8
| 2 |
故答案为8
| 2 |
点评：本题考查了勾股定理和垂径定理，解此类题目要注意将圆的问题转化成三角形的问题再进行计算．
练习册系列答案
阅读快车系列答案
相关题目
20、如图，已知⊙O的半径为5，点A到圆心O的距离为3，则过点A的所有弦中，最短弦的长为（ ）
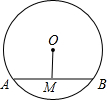如图，已知⊙O的半径为5，OM⊥AB，垂足为M，如果OM=3，则弦AB长为（ ）| A、4 | B、6 | C、7 | D、8 |
已知⊙O的半径为3，△ABC内接于⊙O，AB=3
，AC=3
，D是⊙O上一点，且AD=3，则CD的长应是（ ）
| 2 |
| 3 |
| A、3 | ||
| B、6 | ||
C、
| ||
| D、3或6 |
，AC=3
，D是⊙O上一点，且AD=3，则CD的长应是（ ）