题目内容
(2001•内江)已知⊙O的半径为3,△ABC内接于⊙O,AB=3 ,AC=3
,AC=3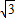 ,D是⊙O上一点,且AD=3,则CD的长应是( )
,D是⊙O上一点,且AD=3,则CD的长应是( )A.3
B.6
C.
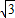
D.3或6
【答案】分析:根据题意,画出草图,此题中点D的位置是不确定的,点D可在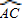 上,也可在
上,也可在 上,所以需分情况讨论.利用等边三角形的判定定理和性质求解.
上,所以需分情况讨论.利用等边三角形的判定定理和性质求解.
解答: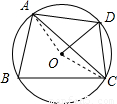 解:第一种情况,当点D在AC弧上时,连接OA、OC、OD.
解:第一种情况,当点D在AC弧上时,连接OA、OC、OD.
所以AD=OA=OC=OD=3,△AOD是等边三角形,∠ADO=∠DAO=∠AOD=60°.
过O作OP垂直弦AC于P,根据垂径定理,PA=PC= AC=
AC=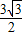 .
.
∴在Rt△AOP中,OP= ,
,
∴∠OAP=30°,∠AOP=60°=∠AOD.
∴OP与OD重合,即OD垂直平分弦AC,所以CD=AD=3.
第二种情况:当点D在AB弧上时,同理得△AOD是等边三角形,∠AOD=60°.
由(1)知∠AOC=120°.
∴∠AOD+∠AOC=180°,即D、O、C在同一直线上,故CD=6.
故选D.
点评:本题考查了等边三角形,垂径定理、勾股定理等知识的应用能力.
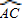 上,也可在
上,也可在 上,所以需分情况讨论.利用等边三角形的判定定理和性质求解.
上,所以需分情况讨论.利用等边三角形的判定定理和性质求解.解答:
 解:第一种情况,当点D在AC弧上时,连接OA、OC、OD.
解:第一种情况,当点D在AC弧上时,连接OA、OC、OD.所以AD=OA=OC=OD=3,△AOD是等边三角形,∠ADO=∠DAO=∠AOD=60°.
过O作OP垂直弦AC于P,根据垂径定理,PA=PC=
 AC=
AC=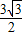 .
.∴在Rt△AOP中,OP=
 ,
,∴∠OAP=30°,∠AOP=60°=∠AOD.
∴OP与OD重合,即OD垂直平分弦AC,所以CD=AD=3.
第二种情况:当点D在AB弧上时,同理得△AOD是等边三角形,∠AOD=60°.
由(1)知∠AOC=120°.
∴∠AOD+∠AOC=180°,即D、O、C在同一直线上,故CD=6.
故选D.
点评:本题考查了等边三角形,垂径定理、勾股定理等知识的应用能力.

练习册系列答案
相关题目
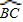 的中点,连接AG交BC于D,过D的直线交AB于E,交AC的延长线于F;
的中点,连接AG交BC于D,过D的直线交AB于E,交AC的延长线于F;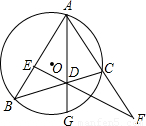
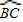 的中点,连接AG交BC于D,过D的直线交AB于E,交AC的延长线于F;
的中点,连接AG交BC于D,过D的直线交AB于E,交AC的延长线于F;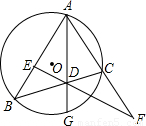

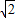 ,AC=3
,AC=3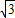 ,D是⊙O上一点,且AD=3,则CD的长应是( )
,D是⊙O上一点,且AD=3,则CD的长应是( )