题目内容
【题目】定义:只有一组对角是直角的四边形叫做损矩形,连结它的两个非直角顶点的线段叫做这个损矩形的直径.
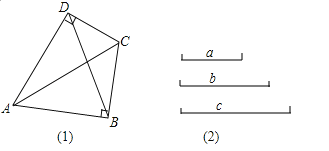
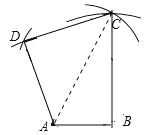
(1)识图:如图(1),损矩形ABCD,∠ABC=∠ADC=90°,则该损矩形的直径线段为 .
(2)探究:在上述损矩形ABCD内,是否存在点O,使得A、B、C、D四个点都在以O为圆心的同一圆上?如果有,请指出点O的具体位置;若不存在,请说明理由.
(3)实践:已知如图三条线段a、b、c,求作相邻三边长顺次为a、b、c的损矩形ABCD(尺规作图,保留作图痕迹).
【答案】(1)AC;(2)答案见解析;(3)答案见解析.
【解析】试题分析:(1)由损矩形的直径的定义即可得到答案;
(2)①由![]() 可判定
可判定![]() 四点共圆,易得圆心是线段AC的中点;
四点共圆,易得圆心是线段AC的中点;![]() 首先画线段AB=a,再以A为圆心,b长为半径画弧,再以B为圆心,c长为半径画弧,过点B作直线与以B为圆心的弧相交与点C,连接AC,以AC的中点为圆心,
首先画线段AB=a,再以A为圆心,b长为半径画弧,再以B为圆心,c长为半径画弧,过点B作直线与以B为圆心的弧相交与点C,连接AC,以AC的中点为圆心, ![]() 为半径画弧,与以点A为圆心的弧交于点D,连接AD、DC,BC即可得到所求图形.
为半径画弧,与以点A为圆心的弧交于点D,连接AD、DC,BC即可得到所求图形.
试题解析:(1)由定义知,线段AC是该损矩形的直径,
故答案为:AC;
(2)∵![]()
∴![]()
∴![]() 四点共圆,
四点共圆,
∴在损矩形ABCD内存在点O,
使得![]() 四个点都在以O为圆心的同一个圆上,
四个点都在以O为圆心的同一个圆上,
∵![]()
∴AC是![]() 的直径,
的直径,
∴O是线段AC的中点;
(3)如图所示, AB=a,AD=b,BC=c,
四边形ABCD即为所求.

 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
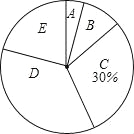
轻巧夺冠周测月考直通名校系列答案【题目】今年5月份,某校九年级学生参加了南宁市中考体育考试,为了了解该校九年级(1)班同学的中考体育情况,对全班学生的中考体育成绩进行了统计,并绘制以下不完整的频数分布表(如表)和扇形统计图(如图),根据图表中的信息解答下列问题:
(1)求全班学生人数和m的值.
(2)直接写出该班学生的中考体育成绩的中位数落在哪个分数段.
(3)该班中考体育成绩满分共有3人,其中男生2人,女生1人,现需从这3人中随机选取2人到八年级进行经验交流,请用“列表法”或“画树状图法”求出恰好选到一男一女的概率.
分组 | 分数段(分) | 频数 |
A | 36≤x<41 | 2 |
B | 41≤x<46 | 5 |
C | 46≤x<51 | 15 |
D | 51≤x<56 | m |
E | 56≤x<61 | 10 |