Ő‚ńŅńŕ»›
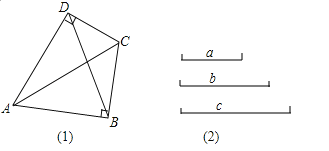
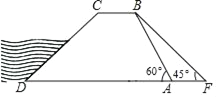
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨Ĺę“ĽłĪ÷ĪĹ«»żĹ«≥ŖĶń÷ĪĹ«∂•Ķ„CĶĢ∑Ň‘ŕ“Ľ∆ū£ģ
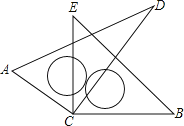
£®1£©»Ű°ŌDCE£Ĺ35°„£¨°ŌACB£Ĺ°° °°£Ľ»Ű°ŌACB£Ĺ140°„£¨‘Ú°ŌDCE£Ĺ°° °°£Ľ
£®2£©≤¬ŌŽ°ŌACB”Ž°ŌDCEĶńīů–°”–ļőŐō ‚ĻōŌĶ£¨≤ĘňĶ√ųņŪ”…£Ľ
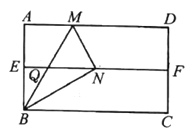
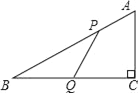
£®3£©»ŰĪ£≥÷»żĹ«≥ŖBCE£®∆š÷–°ŌB£Ĺ45°„£©≤Ľ∂Į£¨»żĹ«≥ŖACDĶńCDĪŖ”ŽCBĪŖ÷ōļŌ£¨»ĽļůĹ껿ū≥ŖACD£®∆š÷–°ŌD£Ĺ30°„£©»∆Ķ„Cįīńś Ī’Ž∑ĹŌÚ»ő“‚◊™∂Į“ĽłŲĹ«∂»°ŌBCD£ģ
…Ť°ŌBCD£Ĺ¶Ń£®0°„£ľ¶Ń£ľ90°„£©
ĘŔ°ŌACBń‹∑Ů «°ŌDCEĶń4Ī∂£Ņ»Űń‹«ů≥Ų¶ŃĶń÷Ķ£Ľ»Ű≤Ľń‹ňĶ√ųņŪ”…£ģ
ĘŕĶĪ’‚ŃĹŅť»żĹ«≥Ŗłų”–“ĽŐűĪŖĽ•ŌŗīĻ÷Ī Ī÷ĪĹ”–ī≥Ų¶ŃĶńňý”–Ņ…ń‹÷Ķ£ģ
°ĺīūįł°Ņ£®1£©145°„£¨40°„£Ľ£®2£©°ŌACB+°ŌDCE£Ĺ180°„ĽÚĽ•≤Ļ£Ľ£®3£©ĘŔĶĪ°ŌACB «°ŌDCEĶń4Ī∂£¨¶Ń£Ĺ54°„£ĽĘŕCE°ÕAD Ī£¨¶Ń£Ĺ30°„£¨BE°ÕCD Ī£¨¶Ń£Ĺ45°„£¨BE°ÕAD Ī£¨¶Ń£Ĺ75°„£ģ
°ĺĹ‚őŲ°Ņ
£®1£©”…”ŕ «ŃĹ÷ĪĹ«»żĹ«–őįŚ÷ōĶĢ£¨÷ōĶĢĶń≤Ņ∑÷ĺÕĪ»90°„+90°„ľű…ŔĶń≤Ņ∑÷£¨ňý“‘»Ű°ŌDCE£Ĺ35°„£¨‘Ú°ŌACBĶń∂» żő™180°„©Ā35°„£Ĺ145°„£¨°ŌACB£Ĺ140°„£¨‘Ú°ŌDCEĶń∂» żő™180°„©Ā140°„£Ĺ40°„
£®2£©”…”ŕ°ŌACD£Ĺ°ŌECB£Ĺ90°„£¨÷ōĶĢĶń∂» żĺÕ «°ŌECDĶń∂» ż£¨ňý“‘°ŌACB+°ŌDCE£Ĺ180°„£ģ
£®3£©ĘŔĶĪ°ŌACB «°ŌDCEĶń4Ī∂£¨…Ť°ŌACB£Ĺ4x£¨°ŌDCE£Ĺx£¨ņŻ”√°ŌACB”Ž°ŌDCEĽ•≤ĻĶ√≥ŲľīŅ…£Ľ
Ęŕ∑÷ĪūņŻ”√CE°ÕAD£¨BE°ÕCD£¨BE°ÕAD∑÷Īū«ů≥ŲľīŅ…£ģ
Ĺ‚£ļ£®1£©°Ŗ°ŌACD£Ĺ°ŌECB£Ĺ90°„£¨°ŌDCE£Ĺ35°„£¨
°ŗ°ŌACB£Ĺ180°„©Ā35°„£Ĺ145°„£ģ
°Ŗ°ŌACD£Ĺ°ŌECB£Ĺ90°„£¨°ŌACB£Ĺ140°„£¨
°ŗ°ŌDCE£Ĺ180°„©Ā140°„£Ĺ40°„£ģ
Ļ īūįłő™£ļ145°„£¨40°„£Ľ
£®2£©°ŌACB+°ŌDCE£Ĺ180°„ĽÚĽ•≤Ļ£¨
ņŪ”…£ļ°Ŗ°ŌACE+°ŌECD+°ŌDCB+°ŌECD£Ĺ180£ģ
°Ŗ°ŌACE+°ŌECD+°ŌDCB£Ĺ°ŌACB£¨
°ŗ°ŌACB+°ŌDCE£Ĺ180°„£¨ľī°ŌACB”Ž°ŌDCEĽ•≤Ļ£ģ
£®3£©ĘŔĶĪ°ŌACB «°ŌDCEĶń4Ī∂£¨
°ŗ…Ť°ŌACB£Ĺ4x£¨°ŌDCE£Ĺx£¨
°Ŗ°ŌACB+°ŌDCE£Ĺ180°„£¨
°ŗ4x+x£Ĺ180°„
Ĺ‚Ķ√£ļx£Ĺ36°„£¨
°ŗ¶Ń£Ĺ90°„©Ā36°„£Ĺ54°„£Ľ
ĘŕCE°ÕAD Ī£¨AD°őBC£¨
°ŗ¶Ń£Ĺ°ŌD=30°„£¨
BE°ÕCD Ī£¨¶Ń£Ĺ¶Ń£Ĺ°ŌB=45°„£¨
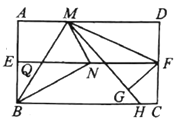
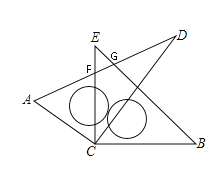
BE°ÕAD Ī£¨»ÁÕľ£¨°ŌEFG=90°„-45°„=45°„£¨
°ŗ°ŌECD=°ŌEFG-°ŌD=45°„-30°„=15°„£¨
‘Ú¶Ń=°ŌECB-°ŌECD=90°„-15°„=75°„.
◊Ř…Ō£¨CE°ÕAD Ī£¨¶Ń£Ĺ30°„£¨BE°ÕCD Ī£¨¶Ń£Ĺ45°„£¨BE°ÕAD Ī£¨¶Ń£Ĺ75°„£ģ

°ĺŐ‚ńŅ°Ņń≥Ļęňĺľ∆ĽģÕ∂»Ž50ÕÚ‘™£¨Ņ™∑Ę≤Ę…ķ≤ķľ◊““ŃĹ÷÷≤ķ∆∑£¨łýĺ› –≥°Ķų≤ť‘§ľ∆ľ◊≤ķ∆∑ĶńńÍĽŮņŻy1£®ÕÚ‘™£©”ŽÕ∂»Ž◊ Ĺūx£®ÕÚ‘™£©≥…’żĪ»ņż£¨““≤ķ∆∑ĶńńÍĽŮņŻy2£®ÕÚ‘™£©”ŽÕ∂»Ž◊ Ĺūx£®ÕÚ‘™£©Ķń∆Ĺ∑Ĺ≥…’żĪ»ņż£¨…Ťł√ĻęňĺÕ∂»Ž““≤ķ∆∑x£®ÕÚ‘™£©£¨ŃĹ÷÷≤ķ∆∑ĶńńÍ◊‹ĽŮņŻő™yÕÚ‘™£®x°›0£©£¨Ķ√ĶĹŃňĪŪ÷–Ķń żĺ›£ģ
x£®ÕÚ‘™£© | 20 | 30 |
y£®ÕÚ‘™£© | 10 | 13 |
£®1£©«ůy”ŽxĶńļĮ żĻōŌĶ Ĺ£Ľ
£®2£©ł√Ļęňĺ÷Ń…ŔŅ…ĽŮĶ√∂ŗ…ŔņŻ»ů£Ņ«Žń„ņŻ”√ňý—ßĶń ż—ß÷™ ∂∂‘ł√ĻęňĺÕ∂»Ž◊ ĹūĶń∑÷ŇšŐŠ≥ŲļŌņŪĽĮĹ®
“ť£¨ ĻňŻń‹ĽŮĶ√◊ÓīůņŻ»ů£¨≤Ę«ů≥Ų◊ÓīůņŻ»ů «∂ŗ…Ŕ£Ņ
£®3£©»Űī”ńÍ◊‹ņŻ»ůŅŘ≥żÕ∂»Ž““≤ķ∆∑◊ ĹūĶńaĪ∂£®a°‹1£©ļů£¨ £”ŗņŻ»ůňśx‘Ųīů∂Ýľű–°£¨«ůaĶń»°÷Ķ
∑∂őߣģ
°ĺŐ‚ńŅ°Ņń≥ňģĻŻŇķ∑Ę…Ő”ŻĹęA –Ķń“ĽŇķňģĻŻ‘ňÕýB –Ōķ Ř£¨”–Ľū≥ĶļÕ∆Ż≥ĶŃĹ÷÷‘ň šĻ§ĺŖ£¨‘ň šĻż≥Ő÷–Ķńňūļńĺýő™160‘™/ Ī°£”–Ļō żĺ›»ÁŌ¬£ļ
‘ň šĻ§ĺŖ | ∆ĹĺýňŔ∂»£®«ß√◊/ Ī£© | ‘ň∑—£®‘™/«ß√◊£© | ◊į–∂∑—£®‘™£© |
Ľū≥Ķ | 100 | 18 | 1800 |
∆Ż≥Ķ | 80 | 22 | 1000 |
£®1£©»ÁĻŻ∆Ż≥ĶĶń◊‹÷ß≥Ų∑—”√Ī»Ľū≥Ķ∑—”√∂ŗ960‘™£¨«ů≥ŲA –”ŽB –÷ģľšĶń¬∑≥Ő «∂ŗ…Ŕ«ß√◊£Ņ«ŽŃ–∑Ĺ≥ŐĹ‚īū°£
£®2£©»ÁĻŻA –”ŽC –÷ģľšĶńĺŗņŽő™300«ß√◊£¨“™ŌŽĹę’‚ŇķňģĻŻ‘ňÕýC –Ōķ Ř°£—°‘Ůńń÷÷‘ň šĻ§ĺŖĪ»ĹŌļŌň„ńō£Ņ«ŽÕ®Ļżľ∆ň„ňĶ√ųń„ĶńņŪ”…°£