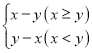题目内容
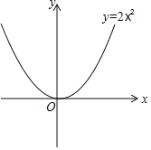
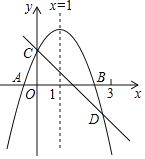
【题目】已知抛物线![]() ,将抛物线在
,将抛物线在![]() 轴左侧部分沿
轴左侧部分沿![]() 轴翻折,翻折后的部分和抛物线与
轴翻折,翻折后的部分和抛物线与![]() 轴交点以及
轴交点以及![]() 轴右侧部分组成图形
轴右侧部分组成图形![]() ,已知
,已知![]()

(1)求抛物线![]() 的对称轴;
的对称轴;
(2)当![]() 时,
时,
①若点![]() 在图形
在图形![]() 上,求
上,求![]() 的值;
的值;
②直接写出线段![]() 与图形
与图形![]() 的公共点个数;
的公共点个数;
(3)当n<0时,若线段![]() 与图形
与图形![]() 恰有两个公共点,直接写出
恰有两个公共点,直接写出![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)①5;②3;3)
;(2)①5;②3;3)![]()
【解析】
(1)根据抛物线的对称轴公式求解即可;
(2)①可先求出点A关于x轴的对称点,再代入已知的抛物线求解;②画出函数图象,结合函数图象即得答案;
(3)根据图象找出线段![]() 与图形
与图形![]() 恰有两个公共点和恰有一个公共点时对应的n的值,问题即得解决.
恰有两个公共点和恰有一个公共点时对应的n的值,问题即得解决.
解:(1)抛物线的对称轴是:直线![]() ;
;
(2)①当n=0时,![]() ,
,
∵A(-1,m)在图形G上,∴A(-1,m)关于x轴的对称点(―1,―m)在![]() 图象上,∴
图象上,∴![]() ,解得:m=5.
,解得:m=5.
② ∵y轴左侧部分的解析式是![]() ,当
,当![]() 时,
时,![]() ,∴线段
,∴线段![]() 与图形
与图形![]() 的公共点个数是3个,如图.:
的公共点个数是3个,如图.:

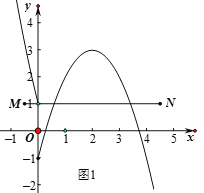
(3)当线段![]() 与图形
与图形![]() 恰有两个公共点时,如图1,此时
恰有两个公共点时,如图1,此时![]() ,
,
当线段![]() 与图形
与图形![]() 恰有一个公共点时,即
恰有一个公共点时,即![]() 的顶点在线段
的顶点在线段![]() 上,如图2,此时
上,如图2,此时![]() ,
,
∴![]() 的取值范围是:
的取值范围是:![]() .
.


练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
【题目】观察下列一组图形,它反映了图形中点的个数与第![]() 个图形之间的某种变化规律.
个图形之间的某种变化规律.
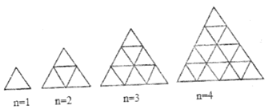
(1)填写下表:
第 | 1 | 2 | 3 | 4 | … |
图形中所有点的个数 | … |
(2)设第![]() 个图形中点的个数是
个图形中点的个数是![]() 个,试写出
个,试写出![]() 与
与![]() 的关系式 .
的关系式 .
(3)若某个图形中所有点的个数是66个,求这是第几个图形?