题目内容
【题目】观察下列一组图形，它反映了图形中点的个数与第
个图形之间的某种变化规律.
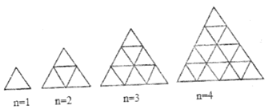
（1）填写下表：
第 | 1 | 2 | 3 | 4 | … |
图形中所有点的个数 | … |
（2）设第个图形中点的个数是
个，试写出与的关系式 ．
（3）若某个图形中所有点的个数是66个，求这是第几个图形？
【答案】（1）3 6 10 15 ；（2）
；（3）10 .
【解析】
（1）由图可知：1个图形点的个数为1+2=3个，第2个图中点的个数为1＋2+3＝6个，3个图形点的个数为1＋2＋3＋4=10，
（2）第n个图形中点的个数为1＋2+3＋…＋n+n＋1＝
（n＋1）（n＋2）个，
（3） 令（n＋1）（n＋2）=66，解方程即可求解.
填写下：
第 | 1 | 2 | 3 | 4 | … |
图形中所有点的个数 | 3 | 6 | 10 | 15 | … |
（2）S=1＋2+3＋…＋n+n＋1＝（n＋1）（n+2）；
(3)令（n＋1）（n＋2）=66
解得n1=10,n2=-13（舍去）
故这是第10个图形.
练习册系列答案
相关题目
