题目内容
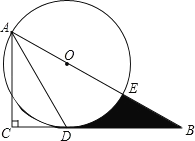
【题目】如图,在![]() 中,已知
中,已知![]() ,
,![]() 是
是![]() 边上一点,
边上一点,![]() ,
,![]() 平分
平分![]() ,分别交
,分别交![]() ,
,![]() 于点
于点![]() ,
,![]() ,连接
,连接![]() .
.

(1)若![]() ,求
,求![]() 和
和![]() 的度数;
的度数;
(2)若![]() ,求证
,求证![]() .
.
【答案】(1)70°;30°;(2)见解析
【解析】
(1)根据等边对等角求出∠CAB和∠CBA的度数,再根据等边对等角求出∠BEC和∠BCE的度数,从而可得出∠ACE的度数,最后根据外角的性质可求出∠BEC的度数;再证明△BCF≌△BEF,从而得出∠BEF的度数,最后得出∠FEC的度数.
(2)先根据(1)中全等得出EF=CF,再由等角对等边判定△AEF为等腰三角形,得出AE=EF,从而得出结果.
证明:(1)∵![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
∵![]() 平分
平分![]() ,∴∠CBF=∠EBF,
,∴∠CBF=∠EBF,
在△BCF和△BEF中,

∴△BCF≌△BEF(SAS).
∴∠BEF=∠BCF=100°,.
∴∠FEC=∠BEF-∠BEC=30°.
(2)由(1)可知![]() ,
,
∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() .
.
∴![]() .
.

练习册系列答案
 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目