题目内容
如图所示,给出下列条件:①∠B=∠ACD; ②∠ADC=∠ACB; ③ ; ④AC2=AD·AB.其中单独能够判定△ABC∽△ACD的有( )
; ④AC2=AD·AB.其中单独能够判定△ABC∽△ACD的有( )
A.①②③④ B.①②③ C.①②④ D.①②
C.
解析试题分析:由图可知△ABC与△ACD中A为公共角,所以只要再找一组角相等,或一组对应边成比例即可解答:
①∠B=∠ACD,再加上∠A为公共角,可以根据有两组角对应相等的两个三角形相似来判定;
②∠ADC=∠ACB,再加上∠A为公共角,可以根据有两组角对应相等的两个三角形相似来判定;
③中∠A不是已知的比例线段的夹角,不正确;
④可以根据两组对应边的比相等且相应的夹角相等的两个三角形相似来判定.
∴单独能够判定△ABC∽△ACD的有①②④. 故选C.
考点:相似三角形的判定.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如图,DE是△ABC的中位线,延长DE至F使EF=DE,连接CF,则S△CEF:S四边形BCED的值为
| A.1∶3 | B.2∶3 | C.1∶4 | D.2∶5 |
如图,△ABC中,AB>AC,D为AB上一点,下列条件:①∠B=∠ACD,②∠ADC=∠ACB,③ ,④
,④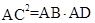 中,能判定△ABC与△ACD相似的有( )
中,能判定△ABC与△ACD相似的有( )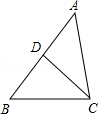
| A.1个 | B.2个 | C.3个 | D.4个 |
如图,将矩形纸片ABCD沿EF折叠,使点B与CD的中点重合,若AB=2,BC=3,则△FCB′与△B′DG的面积之比为( )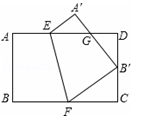
| A.3:2 | B.9:4 | C.4:3 | D.16:9 |
如图,在△ABC中,DE∥BC, ,DE=4,则BC的长为( )
,DE=4,则BC的长为( )
| A.8 | B.12 | C.11 | D.10 |
 中,
中, ,当直角三角板
,当直角三角板 的
的 角的顶点
角的顶点 在
在 上移动时,斜边
上移动时,斜边 始终经过
始终经过 边的中点
边的中点 ,设直角三角板的另一直角边
,设直角三角板的另一直角边 与
与 相交于点E.设
相交于点E.设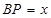 ,
, ,那么
,那么 与
与 之间的函数图象大致是( )
之间的函数图象大致是( )

 AE,垂足为G,BG=
AE,垂足为G,BG=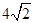 ,则△CEF的周长为( )
,则△CEF的周长为( )





 中,点D、E分别在边AB 、AC上,下列比例式不能判定
中,点D、E分别在边AB 、AC上,下列比例式不能判定 ∥
∥ 的是( ).
的是( ).
 ; B.
; B. ;C.
;C. ;D.
;D. .
.