题目内容
如图,DE是△ABC的中位线,延长DE至F使EF=DE,连接CF,则S△CEF:S四边形BCED的值为
| A.1∶3 | B.2∶3 | C.1∶4 | D.2∶5 |
A.
解析试题分析:先利用SAS证明△ADE≌△CFE(SAS),得出S△ADE=S△CFE,再由DE为中位线,判断△ADE∽△ABC,且相似比为1:2,利用相似三角形的面积比等于相似比,得到S△ADE:S△ABC=1:4,则S△ADE:S四边形BCED=1:3,进而得出S△CEF:S四边形BCED=1:3.
故选A.
考点:相似三角形的判定与性质.

练习册系列答案
相关题目
如图,身高为1.5米的某学生想测量一棵大树的高度,她沿着树影BA由B向A走去当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=3米,CA=1米,则树的高度为( )
| A.3米 | B.4米 | C.4.5米 | D.6米 |
如图,将一张等腰直角三角形纸片沿虚线剪成甲、乙、丙三块,其中甲、丙为直角梯形,乙为等腰直角三角形.根据图中标示的边长数据,比较甲、乙、丙的面积大小,下列判断正确的是( )
| A.甲>乙>丙; | B.乙>丙>甲; | C.丙>乙>甲; | D.丙>甲>乙. |
在同一时刻,身高1.6m的小强,在太阳光线下影长是1.2m,旗杆的影长是15m,则旗杆高为( )
| A.22m | B.20m | C.18m | D.16m |
下列说法中正确的是( )
①在两个边数相同的多边形中,如果对应边成比例,那么这两个多边形相似;
②如果两个矩形有一组邻边对应成比例,那么这两个矩形相似;
③有一个角对应相等的平行四边形都相似;
④有一个角对应相等的菱形都相似.
| A.①② | B.②③ | C.③④ | D.②④ |
已知等边△ 中,
中, ,
, 与
与 相交于点
相交于点 ,则∠
,则∠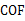 等于( )
等于( )
| A.75° | B.60° | C.55° | D.45° |
若 ,且
,且 ,则
,则 的值是( )
的值是( )
| A.14 | B.42 | C.7 | D.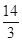 |
 ; ④AC2=AD·AB.其中单独能够判定△ABC∽△ACD的有( )
; ④AC2=AD·AB.其中单独能够判定△ABC∽△ACD的有( )

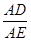 =
=