题目内容
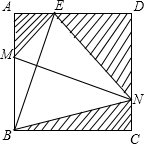 如图,四边形ABCD为正方形,若AB=4,E是AD边上一点(点E与点A、D不重合),BE的中垂线交AB于M,交DC于N,设AE=x,则图中阴影部分的面积S与x的大致图象是( )
如图,四边形ABCD为正方形,若AB=4,E是AD边上一点(点E与点A、D不重合),BE的中垂线交AB于M,交DC于N,设AE=x,则图中阴影部分的面积S与x的大致图象是( )A、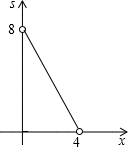 | B、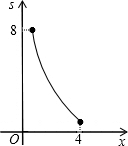 | C、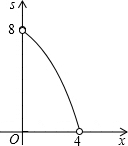 | D、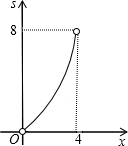 |
分析:根据ABCD是正方形,可以证明BE=MN,阴影部分的面积等于正方形ABCD的面积减去四边形MBNE的面积,得到S关于x的二次函数,然后确定函数的大致图形.
解答:解:在△ABE中,BE=
=
,
∵ABCD是正方形,
∴BE=MN,
∴S四边形MBNE=
BE•MN=
x2+8,
∴阴影部分的面积S=16-(
x2+8)=-
x2+8.
根据二次函数的图形和性质,这个函数的图形是开口向下,对称轴是Y轴,顶点是(0,8),自变量的取值范围是0<x<4.
故选C.
| AB2+AE2 |
| 16+x2 |
∵ABCD是正方形,
∴BE=MN,
∴S四边形MBNE=
| 1 |
| 2 |
| 1 |
| 2 |
∴阴影部分的面积S=16-(
| 1 |
| 2 |
| 1 |
| 2 |
根据二次函数的图形和性质,这个函数的图形是开口向下,对称轴是Y轴,顶点是(0,8),自变量的取值范围是0<x<4.
故选C.
点评:本题考查的是动点问题的函数图象,先根据正方形的性质得到BE=MN,然后表示出S关于x的二次函数,确定二次函数的大致图象.

练习册系列答案
相关题目
 如图,四边形ABCD的对角线AC与BD互相垂直平分于点O,设AC=2a,BD=2b,请推导这个四边形的性质.(至少3条)
如图,四边形ABCD的对角线AC与BD互相垂直平分于点O,设AC=2a,BD=2b,请推导这个四边形的性质.(至少3条) 如图,四边形ABCD的对角线AC、BD交于点P,过点P作直线交AD于点E,交BC于点F.若PE=PF,且AP+AE=CP+CF.
如图,四边形ABCD的对角线AC、BD交于点P,过点P作直线交AD于点E,交BC于点F.若PE=PF,且AP+AE=CP+CF. 如图,四边形ABCD,AB=AD=2,BC=3,CD=1,∠A=90°,求∠ADC的度数.
如图,四边形ABCD,AB=AD=2,BC=3,CD=1,∠A=90°,求∠ADC的度数. 如图,四边形ABCD为正方形,E是BC的延长线上的一点,且AC=CE,求∠DAE的度数.
如图,四边形ABCD为正方形,E是BC的延长线上的一点,且AC=CE,求∠DAE的度数.