题目内容
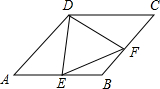
如图所示,在?ABCD中,AC⊥BC,AC=BC=2,动点P从点A出发沿AC向终点C移动,过点P分别作PM∥AB,PN∥AD,连结AM,设AP=x,△AMP的面积为y.
(1)四边形PMCN是不是菱形,请说明理由.
(2)写出y与x之间的函数关系式.

(1)四边形PMCN是不是菱形,请说明理由.
(2)写出y与x之间的函数关系式.

(1)四边形PMCN不可能是菱形,
理由:∵PM∥AB,
∴PM∥CN,
同理可得:PN∥MC,
∴四边形PMCN是平行四边形,
∵AC⊥BC,
∴△PCM为直角三角形,
∴PM>MC,
∴四边形PMCN不可能是菱形;
(2)在△ACB中,
∵CA=CB=2,∠ACB=90°,
∴∠CAB=∠CBA=45°,
又∵PM∥AB,
∴∠CPM=∠CMP=45°,
∴CP=CM,
∴AP=BM=x,
∴MC=BC-BM=2-x,
S△AMP=
AP×MC=
x×(2-x),
∴y与x之间的函数关系式为:y=-
x2+x.
理由:∵PM∥AB,
∴PM∥CN,
同理可得:PN∥MC,
∴四边形PMCN是平行四边形,
∵AC⊥BC,
∴△PCM为直角三角形,
∴PM>MC,
∴四边形PMCN不可能是菱形;
(2)在△ACB中,
∵CA=CB=2,∠ACB=90°,
∴∠CAB=∠CBA=45°,
又∵PM∥AB,
∴∠CPM=∠CMP=45°,
∴CP=CM,
∴AP=BM=x,
∴MC=BC-BM=2-x,
S△AMP=
| 1 |
| 2 |
| 1 |
| 2 |
∴y与x之间的函数关系式为:y=-
| 1 |
| 2 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目