题目内容
【题目】如图,分别以线段AB的两个端点为圆心,大于AB的长为半径作弧,两弧交于M、N两点,连接MN , 交AB于点D、C是直线MN上任意一点,连接CA、CB , 过点D作DE⊥AC于点E , DF⊥BC于点F . 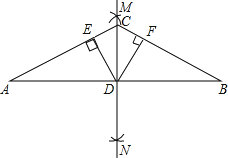
(1)求证:△AED≌△BFD;
(2)若AB=2,当CD的值为多少时,四边形DECF是正方形?
【答案】
(1)
解答:证明:由作图知,MN是线段AB的垂直平分线,∵C是直线MN上任意一点,MN交AB于点D,
∴CA=CB,AD=BD,
∴∠A=∠B,在△AED与△BFD中, 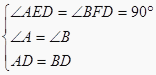 ,
,
∴△AED≌△BFD(AAS).
(2)
解答:解:若AB=2,当CD的值为1时,四边形DECF是正方形.
理由如下:∵AB=2,∴AD=BD= ![]() AB=1.
AB=1.
∵CD=AD=BD=1,MN⊥AB,
∴△ACD与△BCD都是等腰直角三角形,
∴∠ACD=∠BCD=45°,
∴∠ECF=∠ACD+∠BCD=90°,
∵∠DEC=∠DFC=90°,
∴四边形DECF是矩形,∠CDE=90°-45°=45°,
∴∠ECD=∠CDE=45°,
∴ED=CE,
∴矩形DECF是正方形.
【解析】(1)先由作图知MN是线段AB的垂直平分线,根据垂直平分线的性质得出CA=CB , AD=BD , 由等边对等角得到∠A=∠B , 然后利用AAS即可证明△AED≌△BFD;(2)若AB=2,当CD的值为1时,四边形DECF是正方形.先由CD=AD=BD=1,MN⊥AB , 得出△ACD与△BCD都是等腰直角三角形,则∠ACD=∠BCD=45°,∠ECF=90°,根据有三个角是直角的四边形是矩形证明四边形DECF是矩形,再由等角对等边得出ED=CE , 从而得出矩形DECF是正方形.
【考点精析】本题主要考查了线段垂直平分线的性质和正方形的判定方法的相关知识点,需要掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等;先判定一个四边形是矩形,再判定出有一组邻边相等;先判定一个四边形是菱形,再判定出有一个角是直角才能正确解答此题.



