题目内容
【题目】2013年4月20日8时2分在四川省雅安市芦山县发生7.0级地震,有1.8万人等待安置,各地人民纷纷捐款灾区.某市一企业在得知灾区急需帐篷后立即与厂家联系购买帐篷送往灾区.已知用9万元刚好可以从厂家购进帐篷500顶.该厂家生产三种不同规格的帐篷,出厂价分别为甲种帐篷每顶150元,乙种帐篷每顶210元,丙种帐篷每顶250元.
①若企业同时购进其中两种不同规格的帐篷,则企业的购买方案有哪几种?
②若企业想同时购进三种不同规格的帐篷,必须每种帐篷都有,为了便于分类打包,每种帐篷数都要求是10的倍数.请你研究一下是否可行?如果可行请给出符合条件的设计方案;若不可行,请说明理由.
【答案】解:设购买的帐篷数为甲种x顶,乙种y顶,丙种z顶,
①由题意分三种情况讨论:
(i)![]() ,
,
解得:![]() ;
;
(ii)![]() ,
,
解得:![]() (不合题意,舍去),
(不合题意,舍去),
(iii)![]() ,
,
解得:![]() .
.
即有两种方案:甲、乙两种帐篷各250顶;甲种帐篷350顶,丙种帐篷150种;
②由题意得,![]() ,
,
解得: ,
,
∵x,y,z均为大于0且小于500的整数,同时都是10的倍数,
∴x,y,z的取值可以为: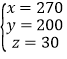 ,
,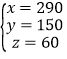 ,
, ,
,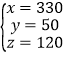 .
.
∴方案可行,符合条件的设计方案有:甲、乙、丙三种帐篷数的配置分别为甲270顶、乙200顶、丙30顶;甲290顶、乙150顶、丙60顶;甲310顶、乙100顶、丙90顶;甲330顶、乙50顶、丙120顶.
【解析】①根据题意设出未知数,找到等量关系,列出方程组;学校同时购进其中两种不同规格的帐篷;可以买甲种和乙种;可以买甲种和丙种;可以买乙种和丙种,分情况讨论,结果要符合实际情况;
②根据题意设出三种帐篷的数量,列出方程组,用一个未知数表示其他两个未知数,在分别计算出符合题意的结果.
【考点精析】解答此题的关键在于理解解三元一次方程组的相关知识,掌握通过“代入”或“加减”消元,把“三元”化为“二元”,使解三元一次方程组转化为解二元一次方程组,进而转化为解一元一次方程.