Question

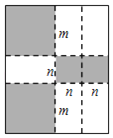
【题目】如图，将一张矩形纸板按图中虚线裁剪成九块，其中有两块是边长都为m的大正方形，两块是边长都为n的小正方形，五块是长为m，宽为n的全等小矩形，且m＞n．（以上长度单位：cm）

（1）观察图形，可以发现代数式2m2+5mn+2n2可以因式分解为　 　；

（2）若每块小矩形的面积为10cm2，两个大正方形和两个小正方形的面积和为58cm2，试求m+n的值

（3）②图中所有裁剪线（虚线部分）长之和为　 　cm．（直接写出结果）

Answer 1

【答案】（1）（2m+n）（m+2n）；（2）7；（3）42

【解析】

（1）根据图象由长方形面积公式将代数式 2m2+5mn+2n2因式分解即可；

（2）根据正方形的面积得出正方形的边长，再利用每块小矩形的面积为10平方厘米，得出等式求出m+n，

（3）根据m+n的值，进一步得到图中所有裁剪线（虚线部分）长之和即可．

解：（1）由图形可知，2m2+5mn+2n2＝（2m+n）（m+2n），

故答案为（2m+n）（m+2n）；

（2）依题意得，2m2+2n2＝58，mn＝10，

∴m2+n2＝29，

∴（m+n）2＝m2+n2+2mn＝29+20＝49，

∴m+n＝7，

故答案为7．

（3）图中所有裁剪线段之和为7×6＝42（cm）．

故答案为42．