Question

【题目】如图，直线y=﹣2x+8分别交x轴，y轴于点A，B，直线yx+3交y轴于点C，两直线相交于点D．

（1）求点D的坐标；

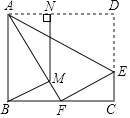
（2）如图2，过点A作AE∥y轴交直线yx+3于点E，连接AC，BE．求证：四边形ACBE是菱形；

（3）如图3，在（2）的条件下，点F在线段BC上，点G在线段AB上，连接CG，FG，当CG=FG，且∠CGF=∠ABC时，求点G的坐标．

Answer 1

【答案】（1）点D坐标(2，4)；（2）证明见详解；（3）点G(，)．

【解析】

(1)两个解析式组成方程组，可求交点D坐标；
(2)先求出点A，点B，点E，点C坐标，由两点距离公式可求BC=AE=AC=BE=5，可证四边形ACBE是菱形；
(3)由“AAS”可证△ACG≌△BGF，可得BG=AC=5，由两点距离公式可求点G坐标．

解：（1）根据题意可得：，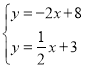

解得：，

∴点D坐标(2，4)

（2）∵直线y=﹣2x+8分别交x轴，y轴于点A，B，

∴点B(0，8)，点A(4，0)．

∵直线yx+3交y轴于点C，

∴点C(0，3)．

∵AE∥y轴交直线yx+3于点E，

∴点E(4，5)

∵点B(0，8)，点A(4，0)，点C(0，3)，点E(4，5)，

∴BC=5，AE=5，AC5，BE5，

∴BC=AE=AC=BE，

∴四边形ACBE是菱形；

（3）∵BC=AC，

∴∠ABC=∠CAB．

∵∠CGF=∠ABC，∠AGF=∠ABC+∠BFG=∠AGC+∠CGF，

∴∠AGC=∠BFG，且FG=CG，∠ABC=∠CAB，

∴△ACG≌△BGF(AAS)，

∴BG=AC=5，

设点G(a，﹣2a+8)，

∴(﹣2a+8﹣8)2+(a﹣0)2=52，

∴a=±，

∵点G在线段AB上，

∴a，

∴点G(，8﹣2)