题目内容
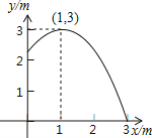
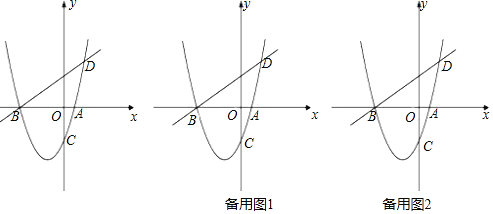
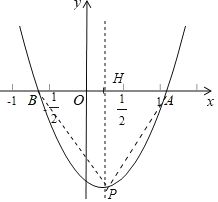
【题目】如图,抛物线y=ax2+bx+c(a,b,c是常数,a≠0)与x轴交于A,B两点,顶点P(m,n).给出下列结论
①2a+c>0;
②若![]() 在抛物线上,则y1>y2>y3
在抛物线上,则y1>y2>y3
③关于x的方程ax2+bx+k=0有实数解,则k>c﹣n;
④当n=﹣![]() 时,△ABP为等腰直角三角形;
时,△ABP为等腰直角三角形;
其中正确结论个数有( )个.
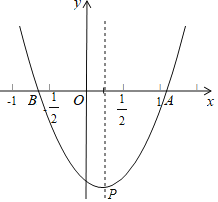
A.1B.2C.3D.4
【答案】C
【解析】
利用二次函数的性质一一判断即可.
∵![]() ,a>0,∴a>﹣b.
,a>0,∴a>﹣b.
∵x=﹣1时,y>0,∴a﹣b+c>0,∴2a+c>a﹣b+c>0,故①正确,
若(![]() ),(
),(![]() ),(
),(![]() ,y3)在抛物线上,
,y3)在抛物线上,
由图象法可知,y1>y2>y3;故②正确.
∵抛物线与直线y=t有交点时,方程ax2+bx+c=t有解,t≥n,∴ax2+bx+c﹣t=0有实数解.
要使得ax2+bx+k=0有实数解,则k=c﹣t≤c﹣n;故③错误,
设抛物线的对称轴交x轴于H.
∵![]() ,∴b2﹣4ac=4,∴x
,∴b2﹣4ac=4,∴x![]() ,∴|x1﹣x2|
,∴|x1﹣x2|![]() ,∴AB=2PH.
,∴AB=2PH.
∵BH=AH,∴PH=BH=AH,∴△PAB是直角三角形.
∵PA=PB,∴△PAB是等腰直角三角形.故④正确.
综上,结论正确的是①②④.
故选C.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目