题目内容
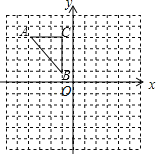
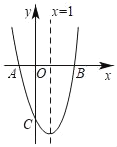
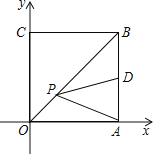
【题目】如图,在平面直角坐标系中,点A,C分别在x轴、y轴上,四边形ABCO是边长为4的正方形,点D为AB的中点,点P为OB上的一个动点,连接DP,AP,当点P满足DP+AP的值最小时,直线AP的解析式为_____.
【答案】y=﹣2x+8
【解析】
根据正方形的性质得到点A,C关于直线OB对称,连接CD交OB于P,连接PA,PD,则此时,PD+AP的值最小,求得直线CD的解析式为y=﹣![]() x+4,由于直线OB的解析式为y=x,解方程组得到P(
x+4,由于直线OB的解析式为y=x,解方程组得到P(![]() ,
,![]() ),由待定系数法即可得到结论.
),由待定系数法即可得到结论.
解:∵四边形ABCO是正方形,
∴点A,C关于直线OB对称,
连接CD交OB于P,连接PA,PD,
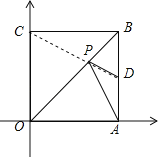
则此时,PD+AP的值最小,
∵OC=OA=AB=4,
∴C(0,4),A(4,0),
∵D为AB的中点,
∴AD=![]() AB=2,
AB=2,
∴D(4,2),
设直线CD的解析式为:y=kx+b,
∴![]() ,
,
∴ ,
,
∴直线CD的解析式为:y=﹣![]() x+4,
x+4,
∵直线OB的解析式为y=x,
∴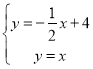 ,
,
解得:x=y=![]() ,
,
∴P(![]() ,
,![]() ),
),
设直线AP的解析式为:y=mx+n,
∴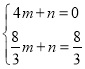 ,
,
解得:![]() ,
,
∴直线AP的解析式为y=﹣2x+8,
故答案为:y=﹣2x+8.

练习册系列答案
相关题目