��Ŀ����
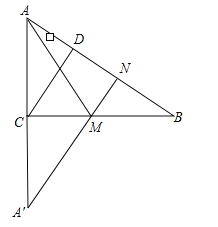
����Ŀ����֪��ABC�У�AC=6cm��BC=8cm��AB=10cm�� CDΪAB���ϵĸߣ�����P�ӵ�A���������š�ABC����������ʱ����һȦ�ص�A�㣬�ٶ�Ϊ2cm/s�����˶�ʱ��Ϊts.
(1) ��CD�ij���
(2) tΪ��ֵʱ����ACPΪ���������Σ�
(3) ��MΪBC��һ���㣬NΪAB��һ���㣬�Ƿ����M��Nʹ��AM+MN��ֵ��С���������߹�����ͼ�Σ���������Сֵ�������û����˵�����ɣ�

���𰸡���1��4.8;(2) 6��8.4��9��9.5;(3)���ڣ���������������
�������������������1�����ݹ��ɶ������涨���жϡ�ABC��ֱ�������Σ����������ε������ʽ���㣻
��2���ֵ�P��BC�Ϻ�P��AB��������������ݵ��������ε��ж��������㣻
��3��������Գ�-���·����������ͼ���ɣ�
���������
��1����AC2+BC2=36+64=100��AB2=100��
��AC2+BC2=AB2��
���ABC��ֱ�������Σ�
��![]() ��AC��BC=
��AC��BC=![]() ��AB��CD��
��AB��CD��
��ã�CD=4.8cm��
��2������P��BC�ϣ�CA=CPʱ��CP=6��
��t=12��2=6s��
����P��AB�ϣ�CA=CPʱ��
��Rt��ADC��AD=![]() =3.6��
=3.6��
��ͼ��

��CA=CP��CDΪAB���ϵĸߣ�
��DP=AP=3.6��
��t=��24��7.2����2=8.4��
��AC=APʱ��t=��24��6����2=9��
��PA=PCʱ��
��ͼ����PH��AC��H��
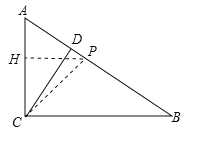
��AH=CH=3��HP=![]() BC=5��
BC=5��
�ɹ��ɶ����ã�AP=5��
��t=��24��5����2=9.5��
�ʵ�t=6��8.4��9��9.5ʱ����ACPΪ���������Σ�
��3����ͼ����A�����BC�ĶԳƵ�A������A����AB�Ĵ���A��N������ΪN����BC��M�㣬M��N��Ϊ����