��Ŀ����
����Ŀ��ij������50�����乩�ο;�ס����ÿ�����䶨��120Ԫʱ�������ȫ��ס������ÿ������ÿ��Ķ���ÿ����10Ԫʱ���ͻ���һ��������У�����ο;�ס���䣬�������ÿ������ÿ��֧��20Ԫ�ĸ��ַ��ã���ÿ�����䶨������10xԪ��xΪ��������
��1��ֱ��д��ÿ���ο;�ס�ķ�������y��x�ĺ�����ϵʽ��
��2�������ÿ�������ΪWԪ����ÿ�䷿�۶���Ϊ����Ԫʱ������ÿ���������������������Ƕ��٣�
��3��ij�գ������˽���ס��������õ�������Ϣ���ٵ�������������5000Ԫ���ڱ���Ϊ�ο;�ס�ķ��乲֧������û�г���600Ԫ����ÿ������պ�ס��2�ˣ��ʣ����������ס���ο����������ж����ˣ�
���𰸡���1��y=50��x����0��x��50����xΪ����������2����ÿ�䷿�۶���Ϊ320Ԫʱ������ÿ����������������������9000Ԫ����3��20��
��������
�����������1������ÿ���ο;�ס�ķ�����������50�����ٵķ��������ɽ�����⣮
��2���������κ��������ö��κ��������ʽ�����⣮
��3�����������г�����ʽ�鼴�ɽ�����⣮
�����������1���������⣬�ã�y=50��x����0��x��50����xΪ��������
��2��W=��120+10x��20����50��x��=![]()
��a=��10��0������x=20ʱ��Wȡ�����ֵ��W���ֵ=9000Ԫ��
�𣺵�ÿ�䷿�۶���Ϊ320Ԫʱ������ÿ����������������������9000Ԫ��
��3����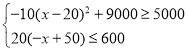 �����20��x��40��
�����20��x��40��
��x=40ʱ�����������ס���ο��������٣���������Ϊ2y=2����x+50��=20���ˣ���

 ���㼤�������100�ִ��Ծ�ϵ�д�
���㼤�������100�ִ��Ծ�ϵ�д�