题目内容
【题目】如图,△ABC与△A1B1C1关于点O成中心对称,下列结论: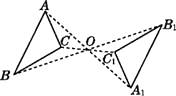
①∠BAC=∠B1A1C1;
②AC=A1C1;
③OA=OA1;
④△ABC与△A1B1C1的面积相等,
其中正确的有( )
A.1个
B.2个
C.3个
D.4个
【答案】D
【解析】解:∵△ABC与△A1B1C1关于点O成中心对称,
∴△ABC≌△A1B1C1 , OA=OA1 ,
∴∠BAC=∠B1A1C1、AC=A1C1 , △ABC与△A1B1C1的面积相等,
∴①②③④正确。
所以答案是:D
【考点精析】关于本题考查的全等三角形的性质和旋转的性质,需要了解全等三角形的对应边相等; 全等三角形的对应角相等;①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了才能得出正确答案.

练习册系列答案
相关题目
【题目】某校共有1000名学生,为了了解他们的视力情况,随机抽查了部分学生的视力,并将调查的数据整理绘制成直方图和扇形图.
(1)这次共调查了多少名学生?扇形图中的a、b值分别是多少?
(2)补全频数分布直方图;
(3)在光线较暗的环境下学习的学生占对应被调查学生的比例如下表:
视力 | ≤0.35 | 0.35~0.65 | 0.65~0.95 | 0.95~1.25 | 1.25~1.55 |
比例 |
|
|
|
|
|
根据调查结果估计该校有多少学生在光线较暗的环境下学习?




